Bài tập 3 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST

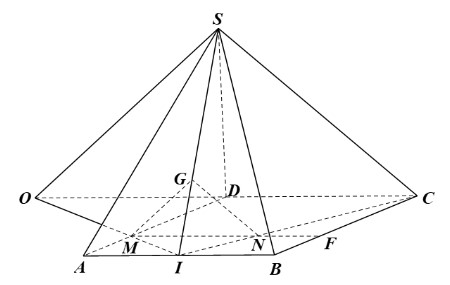
a) Gọi F là giao điểm của MN và BC.

Ta có MN // AB, suy ra NF // BI (vì F ∈ MN, I ∈ AB).

Trong ∆CIB có NF // BI, nên theo định lí Thalès ta có: $\frac{IN}{IC}=\frac{BF}{BC}$ (1)

Mặt khác, AM = $\frac{1}{3}$AD suy ra $\frac{AM}{AD}=\frac{1}{3}$

Lại có MF // AB // DC nên $\frac{BF}{CF}=\frac{AM}{AD}=\frac{1}{3}$ (2)

Từ (1) và (2) suy ra $\frac{NI}{CI}=\frac{BF}{BC}=\frac{1}{3}$

Trong ∆SAB, ta có G là trọng tâm nên $\frac{IG}{IS}=\frac{1}{3}$.

Trong ∆SIC, ta có $\frac{GI}{SI}=\frac{NI}{CI}=\frac{1}{3},$ suy ra GN // SC (định lí Thalès đảo).

Mà SC ⊂ (SDC), do đó NG // (SDC).

b) Trong mặt phẳng (ABCD), gọi O là giao điểm của MI và DC.

Trong ∆OCI có MN // OC (do O ∈ DC), suy ra $\frac{IM}{IO}=\frac{IN}{IC}=\frac{1}{3}$ (theo định lí Thalès).

Mà $\frac{IG}{IS}=\frac{1}{3}$ (G là trọng tâm của ∆SAB).

Do đó, trong ∆SOI có $\frac{IM}{IO}=\frac{IG}{IS}=\frac{1}{3}$, suy ra MG // OS (định lí Thalès đảo).

Mà OS ⊂ (SDC), do đó MG // (SDC).

-- Mod Toán 11 HỌC247