Hoạt động khám phá 3 trang 109 SGK Toán 11 Chân trời sáng tạo tập 1
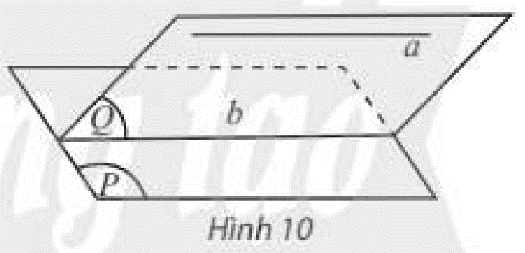
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
Hướng dẫn giải chi tiết Hoạt động khám phá 3
Phương pháp giải:
Để xác định vị trí tương đối của hai đường thẳng, ta dựa vào số điểm chung của hai đường thẳng đó.
Lời giải chi tiết:
Ta có: \(a\parallel \left( P \right) \Rightarrow \) Đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) không có điểm chung.
\(\left( P \right) \cap \left( Q \right) = b \Rightarrow b \subset \left( P \right)\)
Do đó hai đường thẳng \(a,b\) không có điểm chung.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Thực hành 2 trang 109 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 109 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 110 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 111 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 111 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 111 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 121 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 121 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST





