Giải bài 1.14 tr 21 SBT Hình học 11
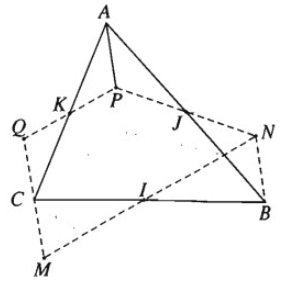
Cho ba điểm không thẳng hàng I, J, K. Hãy dựng tam giác ABC nhận I, J, K lần lượt là trung điểm của các cạnh BC, AB, AC.
Hướng dẫn giải chi tiết
Giả sử tam giác ABC đã dựng được.
Cách dựng điểm C: Lấy điểm M bất kì. Gọi N là ảnh của M qua phép đối xứng tâm I. P là ảnh của N qua phép đối xứng tâm J. Q là ảnh của P qua phép đối xứng tâm K. Khi đó \(\overrightarrow {CM} = - \overrightarrow {BN} = \overrightarrow {AP} = - \overrightarrow {CQ} \). Do đó C là trung điểm của QM.
Tương tự, cách dựng điểm B: Lấy điểm O bất kỳ, gọi O1 là ảnh của O qua J, O2 là ảnh của O1 qua K, O3 là ảnh của O2 qua I, B là trung điểm của OO3.
Cách dựng điểm A: Lấy điểm H bất kỳ, gọi H1 là ảnh của H qua J, H2 là ảnh của H1 qua K, H3 là ảnh của H2 qua I, A là trung điểm của HH3. Từ đó suy ra cách dựng tam giác ABC.
-- Mod Toán 11 HỌC247
-


Trong mặt phẳng Oxy cho điểm M(-3;7). Phép đối xứng tâm O biến M thành M’ thì tọa độ M’ là:
bởi Việt Long
 22/01/2021
22/01/2021
A. M’(-3;-7)
B. M’(3;-7)
C. M’(7;-3)
D. M’(7;3)
Theo dõi (0) 1 Trả lời -


Hình có hai đường thẳng a và b song song với nhau thì có bao nhiêu phép đối xứng tâm biến a thành b?
bởi Bin Nguyễn
 22/01/2021
22/01/2021
A. Một
B. Hai
C. Ba
D. Vô số
Theo dõi (0) 1 Trả lời