Bài tập 17 trang 19 SGK Hình học 11 NC
Cho hai điểm cố định B, C trên đường tròn (O;R) và một điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng tâm để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định
Hướng dẫn. Gọi I là trung điểm BC . Hãy vẽ đường kính AM của đường tròn rồi chứng minh rằng I là trung điểm của đoạn thẳng HM
Hướng dẫn giải chi tiết
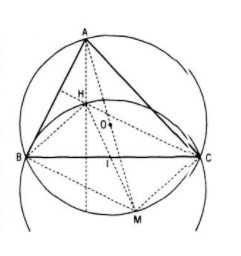
Ta vẽ đường kính AM của đường tròn. Khi đó BH // MC ( vì cùng vuông góc với AC) hay BHCM là hình bình hành
Nếu gọi I là trung điểm của BC thì I cố định và cũng là trung điểm của MH
Vậy phép đối xứng qua điểm I biến M thành H. Khi A chạy trên đường tròn (O; R) thì M chạy trên đường tròn (O;R). Do đó, H nằm trên đường tròn là ảnh của đường tròn (O; R) qua phép đối xứng tâm với tâm I.
-- Mod Toán 11 HỌC247
-


1. A. Có phép đối xứng tâm có 2 điểm biến thành chính nó. B. Phép đối xứng tâm có đúng một điểm biến thành chính nó. C. Phép đối xứng tâm không có điểm nào biến thành chính nó. D. Có phép đối xứng tâm có vô số điểm biếng thành chính nó. 2. Một hình có vô số trục đối xứng thì hình đó phải là đường tròn. B. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm những đường tròn đồng tâm. C. Một hình có vô số trục đối xứng thì hình đó phải là hình gồm hai đường thẳng vuông góc. D. Đường tròn là hình có vô số trục đối xứng
Theo dõi (0) 2 Trả lời






