Hướng dẫn Giải bài tập Toán 10 Cánh Diều Chương 7 Bài 2 Biểu thức tọa độ của các phép toán vectơ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động 1 trang 67 SGK Toán 10 Cánh diều tập 2 - CD
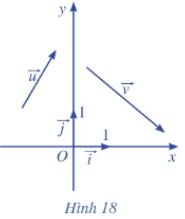
Trong mặt phẳng toạ độ Oxy (Hình 18), cho hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\) và \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\)
a) Biểu diễn các vectơ \(\overrightarrow u ,\overrightarrow v \) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)
b) Biểu diễn các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)
c) Tìm tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)
-
Luyện tập 1 trang 68 SGK Toán 10 Cánh diều tập 2 - CD
a) Cho \(\overrightarrow u = \left( { - 2;0} \right),\overrightarrow v = \left( {0;6} \right),\overrightarrow w = \left( { - 2;3} \right)\). Tìm tọa độ vectơ \(\overrightarrow u + \overrightarrow v + \overrightarrow w \)
b) Cho \(\overrightarrow u = \left( {\sqrt 3 ;0} \right),\overrightarrow v = \left( {0;\sqrt 7 } \right)\). Tìm tọa độ của vectơ \(\overrightarrow w \)sao cho \(\overrightarrow w + \overrightarrow u = \overrightarrow v \)
-
Luyện tập 2 trang 68 SGK Toán 10 Cánh diều tập 2 - CD
Trong bài toán mở đầu, hãy tìm tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 2 giờ.
-
Hoạt động 2 trang 69 SGK Toán 10 Cánh diều tập 2 - CD
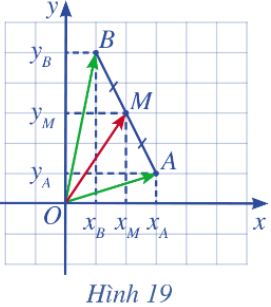
Trong mặt phẳng tọa độ Oxy, cho hai điểm \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\). Gọi \(M\left( {{x_M},{y_M}} \right)\) là trung điểm của đoạn thẳng AB ( minh họa hình 19)
a) Biểu diễn vectơ \(\overrightarrow {OM} \) theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \)
b) Tìm tọa độ của M theo tọa độ của A và B
-
Hoạt động 3 trang 69 SGK Toán 10 Cánh diều tập 2 - CD
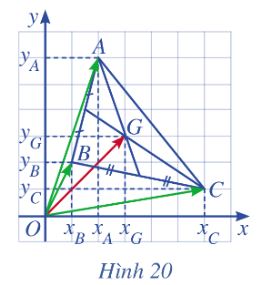
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trọng tâm G ( minh họa ở Hình 20)
a) Biểu diễn vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \) , \(\overrightarrow {OB} \)và \(\overrightarrow {OC} \)
b) Tìm tọa độ G theo tọa độ của A, B, C
-
Luyện tập 3 trang 69 SGK Toán 10 Cánh diều tập 2 - CD
Cho hai điểm A(2; 4) và M(5 ; 7). Tìm toạ độ điểm B sao cho M là trung điểm đoạn thẳng AB.
-
Luyện tập 4 trang 69 SGK Toán 10 Cánh diều tập 2 - CD
Cho ba điểm A(-1; 1), B(1;5), G(1 ; 2).
a) Chứng minh ba điểm A, B, G không thẳng hàng.
b) Tìm toạ độ điểm C sao cho G là trọng tâm của tam giác ABC.
-
Hoạt động 4 trang 70 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho \(\overrightarrow i \) và \(\overrightarrow j \) là vectơ đơn vị trên trục hoành Ox và ở trên trục tung Oy
a) Tính \({\overrightarrow i ^2};{\overrightarrow j ^2};\overrightarrow i .\overrightarrow j .\)
b) Cho \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\). Tính tích vô hướng \(\overrightarrow u .\overrightarrow v \) .
-
Giải bài 1 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow a = \left( { - 1;2} \right),\overrightarrow b = \left( {3;1} \right),\overrightarrow c = \left( {2; - 3} \right)\).
a) Tìm tọa độ của vectơ \(\overrightarrow u = 2\overrightarrow a + \overrightarrow b - 3\overrightarrow c \)
b) Tìm tọa độ của vectơ \(\overrightarrow x \) sao cho \(\overrightarrow x + 2\overrightarrow b = \overrightarrow a + \overrightarrow c \)
-
Giải bài 2 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho A(-2;3), B(4; 5), C(2;- 3).
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm toạ độ trọng tâm G của tam giác ABC.
c) Giải tam giác ABC (làm tròn các kết quả đến hàng đơn vị).
-
Giải bài 3 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trung điểm các cạnh BC, CA, AB tương ứng là M(2 ; 0), N4 ; 2), P(1 ; 3).
a) Tìm toạ độ các điểm A, B, C.
b) Trọng tâm hai tam giác ABC và MNP có trùng nhau không? Vì sao?
-
Giải bài 4 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(2;4), B(-1;1), C(-8; 2).
a) Tính số đo góc ABC (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).
b) Tính chu vi của tam giác ABC.
c) Tìm toạ độ điểm M trên đường thẳng BC sao cho diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM.
-
Giải bài 5 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Cho ba điểm A(1; 1), B(4;3) và C(0;- 2).
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm toạ độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD= 2AB.
-
Giải bài 6 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Chứng minh khẳng định sau: Hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương khi và chỉ khi có một số thực k sao cho \({x_1}{\rm{ = }}k{x_2}\) và \({y_1} = {\rm{ }}k{y_2}\) .
-
Giải bài 7 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
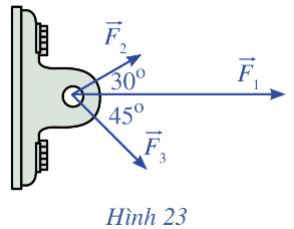
Một vật đồng thời bị ba lực tác động: lực tác động thứ nhất \(\overrightarrow {{F_1}} \) có độ lớn là 1 500 N, lực tác động thứ hai\(\overrightarrow {{F_2}} \) , có độ lớn là 600 N, lực tác động thứ ba\(\overrightarrow {{F_3}} \) , có độ lớn là 800 N. Các lực này được biểu diễn bằng những vectơ như Hình 23, với \(\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_2}} } \right)\) = 30°, \(\left( {\overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {{F_3}} } \right)\)= 45° và \(\left( {\overrightarrow {{F_2}} ,{\rm{ }}\overrightarrow {{F_3}} } \right)\)= 75°. Tính độ lớn lực tổng hợp tác động lên vật (làm tròn kết quả đến hàng đơn vị).
-
Giải bài 12 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Cho hai vectơ \(\overrightarrow u = ( - 1;3)\) và \(\overrightarrow v = (2; - 5)\). Toạ độ của vectơ \(\overrightarrow u + \overrightarrow v \) là:
A. (1; -2)
B. (-2; 1)
C. (-3; 8)
D. (3; -8)
-
Giải bài 13 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Cho hai vectơ \(\overrightarrow u = (2; - 3)\)và \(\overrightarrow v = (1;4)\). Toạ độ của vectơ \(\overrightarrow u - 2\overrightarrow v \) là:
A. (0; 11)
B. (0; -11)
C. (-11; 0)
D. (-3; 10)
-
Giải bài 14 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Cho hai điểm A(4; − 1) và B(– 2; 5). Toạ độ trung điểm M của đoạn thẳng AB là:
A. (2;4)
B. (-3; 3)
C. (3; -3)
D. (1; 2)
-
Giải bài 15 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Cho tam giác ABC có A(4 ; 6), B(1 ; 2), C(7 ; – 2). Toạ độ trọng tâm G của tam giác ABC là:
\(A\left( {4;\frac{{10}}{3}} \right)\)
B. (8; 4)
C. (2;4)
D. (4; 2).
-
Giải bài 16 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Cho hai điểm M(− 2 ; 4) và N(1 ; 2). Khoảng cách giữa hai điểm M và N là:
A. \(\sqrt {13} \)
B. \(\sqrt 5 \)
C. 13
D. \(\sqrt {37} \)
-
Giải bài 17 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Cho hai vectơ \(\overrightarrow u = ( - 4; - 3)\) và \(\overrightarrow v = ( - 1; - 7)\). Góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là:
A. 90⁰
B. 60⁰
C. 45⁰
D. 30⁰
-
Giải bài 18 trang 67 SBT Toán 10 Cánh diều tập 2 - CD
Côsin của góc giữa hai vectơ \(\overrightarrow u = (1;1)\) và \(\overrightarrow v = ( - 2;1)\) là:
A. \( - \frac{1}{{10}}\)
B. \(\frac{{\sqrt {10} }}{{10}}\)
C. \( - \frac{{\sqrt {10} }}{{10}}\)
D. \(\frac{3}{{10}}\)
-
Giải bài 19 trang 67 SBT Toán 10 Cánh diều tập 2 - CD
Cho tam giác ABC có A(2 ; 6), B(– 2 ; 2), C(8 ; 0). Khi đó, tam giác ABC là:
A. Tam giác đều
B. Tam giác vuông tại A
C. Tam giác có góc tù tại A
D. Tam giác cân tại A
-
Giải bài 20 trang 67 SBT Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(1; 5), B(–1; –1), C(2; – 5).
a) Chứng minh ba điểm A, B, C không thẳng hàng
b) Tìm toạ độ trọng tâm G của tam giác ABC
c) Tìm toạ độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD = \(\frac{3}{2}\)AB
-
Giải bài 21 trang 67 SBT Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(– 2 ; 4), B(– 5 ; − 1), C(8 ; – 2). Giải tam giác ABC (làm tròn các kết quả số đo góc đến hàng đơn vị).
-
Giải bài 22 trang 67 SBT Toán 10 Cánh diều tập 2 - CD
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(4 ; −2), B(10; 4) và điểm M nằm trên trục Ox. Tìm toạ độ điểm M sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) có giá trị nhỏ nhất.
-
Giải bài 23 trang 67 SBT Toán 10 Cánh diều tập 2 - CD
Trên màn hình ra đa của đài kiểm soát không lưu (được coi như mặt phẳng toạ độ Oxy với đơn vị trên các trục tính theo ki-lô-mét), một máy bay trực thăng chuyển động thẳng đều từ thành phố A có toạ độ
(600 ; 200) đến thành phố B có toạ độ (200 ; 500) và thời gian bay quãng đường AB là 3 giờ. Hãy tìm toạ độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ.