Hoạt động 1 trang 67 SGK Toán 10 Cánh diều tập 2
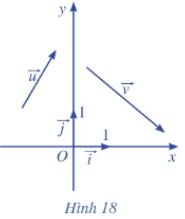
Trong mặt phẳng toạ độ Oxy (Hình 18), cho hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\) và \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\)
a) Biểu diễn các vectơ \(\overrightarrow u ,\overrightarrow v \) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)
b) Biểu diễn các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)
c) Tìm tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)
Hướng dẫn giải chi tiết Hoạt động 1
Phương pháp giải
Cho hai vectơ \(\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right)\) và số thưucj k. Khi đó:
\(\begin{array}{l}
1)\;\;\;\overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1};{a_2} + {b_2}} \right);\\
2)\;\;\;\overrightarrow a - \overrightarrow b = \left( {{a_1} - {b_1};{a_2} - {b_2}} \right);\\
3)\;\;\;k\overrightarrow a = \left( {k{a_1};k{a_2}} \right);\\
4)\;\;\;\overrightarrow a .\overrightarrow b = {a_1}.{b_1} + {a_2}.{b_2}.
\end{array}\)
Hướng dẫn giải
a) Do \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) nên \(\overrightarrow u = {x_1}\overrightarrow i + {y_1}\overrightarrow j .\), \(\overrightarrow v = {x_2}\overrightarrow i + {y_2}\overrightarrow j .\)
b) +) \(\overrightarrow u + \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) + \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i + {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j + {y_2}\overrightarrow j } \right) = \left( {{x_1} + {x_2}} \right)\overrightarrow i + \left( {{y_1} + {y_2}} \right)\overrightarrow j \)
+) \(\overrightarrow u - \overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right) - \left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i - {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j - {y_2}\overrightarrow j } \right) = \left( {{x_1} - {x_2}} \right)\overrightarrow i + \left( {{y_1} - {y_2}} \right)\overrightarrow j \)
+) \(k\overrightarrow u = \left( {k{x_1}} \right)\overrightarrow i + \left( {k{y_1}} \right)\overrightarrow j \)
c) Tọa độ của các vectơ \(\overrightarrow u + \overrightarrow v \),\(\overrightarrow u - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)lần lượt là:
\(\left( {{x_1} + {x_2};{y_1} + {y_2}} \right),\left( {{x_1} - {x_2};{y_1} - {y_2}} \right),\left( {k{x_1},k{y_1}} \right)\)
-- Mod Toán 10 HỌC247
-


Cho bốn điểm \(A\left( {7; - 3} \right),B\left( {8;4} \right),C\left( {1;5} \right),D\left( {0; - 2} \right)\). Chứng minh rằng tứ giác ABCD là hình vuông.
bởi Nguyễn Vân
 18/09/2022
Theo dõi (0) 1 Trả lời
18/09/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Luyện tập 1 trang 68 SGK Toán 10 Cánh diều tập 2 - CD
Luyện tập 2 trang 68 SGK Toán 10 Cánh diều tập 2 - CD
Hoạt động 2 trang 69 SGK Toán 10 Cánh diều tập 2 - CD
Hoạt động 3 trang 69 SGK Toán 10 Cánh diều tập 2 - CD
Luyện tập 3 trang 69 SGK Toán 10 Cánh diều tập 2 - CD
Luyện tập 4 trang 69 SGK Toán 10 Cánh diều tập 2 - CD
Hoạt động 4 trang 70 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 1 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 2 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 3 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 4 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 5 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 6 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 7 trang 72 SGK Toán 10 Cánh diều tập 2 - CD
Giải bài 12 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 13 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 14 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 15 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 16 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 17 trang 66 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 18 trang 67 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 19 trang 67 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 20 trang 67 SBT Toán 10 Cánh diều tập 2 - CD
Giải bài 21 trang 67 SBT Toán 10 Cánh diều tập 2 - CD