Giải bài tập Toán 10 Cánh Diều Bài tập cuối chương 7

Trong mặt phẳng tọa độ Oxy, cho A(3;4); B(2; 5). Tọa độ của \(\overrightarrow{AB}\) là:

A. (1;-1)           

B. (1;1)             

C.(-1;1)         

D.(-1;-1)

Vectơ nào sau đây là một vecto pháp tuyến của đường thẳng \(\Delta :2x-3y+4=0\) ?

A. \(\overrightarrow{{{n}_{1}}}=(3;2)\)

B. \(\overrightarrow{{{n}_{2}}}=(2;3)\)

C. \(\overrightarrow{{{n}_{3}}}=(3;-2)\)

D. \(\overrightarrow{{{n}_{4}}}=(2;-3)\)

Tọa độ tâm I của đường tròn (C): \({{\left( x+6 \right)}^{2}}+{{\left( y-12 \right)}^{2}}=81\) là:

A. (6;-12)              B. (-6;12)              C. (-12;6)              D.(12;-6)

Khoảng cách từ điểm A(1;1) đến đường thẳng \(\Delta :3x+4y+13=0\) bằng:

A. 2                      B.2     

C.3                       D.4

Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có M(2;1); N(-1;3); P(4;-2)

a. Tìm tọa độ của các vectơ \(\overrightarrow{OM};\overrightarrow{MN},\overrightarrow{MP}\)

b. Tính tích vô hướng \(\overrightarrow{MN}.\overrightarrow{MP}\)

c. Tính độ dài các đoạn thẳng MN,MP

d. Tính \(\cos \widehat{NMP}\)

e. Tìm tọa độ trung điểm I của NP và trọng tâm G của tam giác MNP.

 Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:

a. d đi qua điểm A(-3;2) và có một vectơ pháp tuyến là \(\overrightarrow{n}=(2;-3)\)

b. d đi qua điểm B(-2; -5) và có một vectơ chỉ phương là \(\overrightarrow{u}=(-7;6)\)

c. d đi qua hai điểm C(4;3) và D(5;2)

Lập phương trình đường tròn (C) trong mỗi trường hợp sau:

a. (C) có tâm I(-4;2) và bán kính R = 3

b. (C) có tâm P(3;-2) và đi qua điểm E(1;4)

c. (C) có tâm Q(5;-1) và tiếp xúc với đường thẳng \(\Delta :3x+4y-1=0\)

d. (C) đi qua ba điểm A(-3;2); B(-2; -5)  và D(5;2).

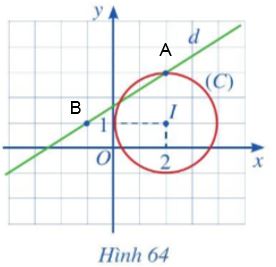
Quan sát Hình 64 và thực hiện các hoạt động sau:

a. Lập phương trình đường thẳng d

b. Lập phương trình đường tròn (C)

c. Lập phương trình tiếp tuyến của đường tròn (C) tại điểm \(M(2+\sqrt{2};1+\sqrt{2})\) 

Cho hai đường thẳng:

\({{\Delta }_{1}}:\sqrt{3}x+y-4=0\) ; \({{\Delta }_{2}}:x+\sqrt{3}y-2\sqrt{3}=0\)

a. Tìm tọa độ giao điểm của hai đường thẳng \({{\Delta }_{1}}\) và \({{\Delta }_{2}}\)

b. Tính số đo góc giữa hai đường thẳng \({{\Delta }_{1}}\) và \({{\Delta }_{2}}\).

Cho biết mỗi đường conic có phương trình dưới đây là đường conic dạng nào (elip, hypebol, parabol) và tìm tọa độ tiêu điểm của đường conic đó.

a. \({{y}^{2}}=18x\)

b. \(\frac{{{x}^{2}}}{64}+\frac{{{y}^{2}}}{25}=1\)

c. \(\frac{{{x}^{2}}}{9}-\frac{{{y}^{2}}}{16}=1\)

Cho tam giác \(A{{F}_{1}}{{F}_{2}}\), trong đó A(0;4) ; \({{F}_{1}}(-3;0)\) ; \({{F}_{2}}(3;0)\).

a. Lập phương trình tổng quát của các đường thẳng \(A{{F}_{1}}\) và \(A{{F}_{2}}\)

b. Lập phương trình đường tròn ngoại tiếp của tam giác \(A{{F}_{1}}{{F}_{2}}\). 

c. Lập phương trình chính tắc của elip (E) có hai tiêu điểm là \({{F}_{1}}\); \({{F}_{2}}(3;0)\) sao cho (E) đi qua A.

Trong mặt phẳng toạ độ Oxy, cho A(–2 ; 1), B(1 ; –3). Toạ độ của vectơ \(\overrightarrow {AB} \) là:

A. (1 ; -4)                   

B. (-3 ; 4)                   

C. (3 ; -4)                   

D. (1 ; -2)

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(− 1 ; − 5), B(5 ; 2) và trọng tâm là gốc toạ độ. Toạ độ điểm C là:

A. (4 ; -3)                   

B. (-4 ; -3)                  

C. (-4 ; 3)                   

D. (4 ; 3)

Trong mặt phẳng toạ độ Oxy, vectơ nào sau đây có độ dài bằng 1?

A. \(\overrightarrow a  = (1;1)\)                 

B. \(\overrightarrow b  = \left( {\frac{1}{2}; - \frac{1}{2}} \right)\)            

C. \(\overrightarrow c  = \left( {\frac{1}{{\sqrt 3 }};\frac{2}{3}} \right)\)                      

D. \(\overrightarrow d  = \left( {\frac{1}{{\sqrt 2 }}; - \frac{{\sqrt 2 }}{2}} \right)\)

Trong mặt phẳng toạ độ Oxy, đường thẳng ∆ đi qua điểm M(–2 ; 0) và song song với đường thẳng d: 2x - y + 2 = 0 có phương trình là:

A. 2x – y = 0              

B. 2x – y + 4 = 0        

C. 2x + y + 4 = 0        

D. x + 2y + 2 = 0

Trong mặt phẳng toạ độ Oxy, cho hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 2 + \sqrt 3 t\\y =  - 1 + 3t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 3 - \sqrt 3 t'\\y =  - t'\end{array} \right.\) Số đo góc giữa hai đường thẳng ∆₁ và ∆₂ là:

A. 30⁰                         

B. 45⁰               

C. 90⁰                         

D. 60⁰

Khoảng cách từ điểm M(4 ; –2) đến đường thẳng ∆: x − 2y + 2 = 0 bằng:

A. \(\frac{{2\sqrt 5 }}{5}\)          

B. \(2\sqrt 5 \)           

C. 2.               

D. \(\sqrt 5 \)

Phương trình nào dưới đây là phương trình đường tròn?

A. (x + 3)² - (y + 4)² = 100           

B. (x + 3)² + (y + 4)² = 100

C. 2(x + 3)² + (y + 4)² = 100              

D. (x + 3)² + 2(y + 4)² = 100

Phương trình nào dưới đây là phương trình chính tắc của đường hypebol?

A. \(\frac{{{x^2}}}{{{{15}^2}}} + \frac{{{y^2}}}{{{{15}^2}}} = 1\)           

B. \(\frac{{{x^2}}}{{{{15}^2}}} + \frac{{{y^2}}}{{{{16}^2}}} =  - 1\)

C. \(\frac{{{x^2}}}{{{{16}^2}}} + \frac{{{y^2}}}{{{{15}^2}}} = 1\)   

D. \(\frac{{{x^2}}}{{{{15}^2}}} - \frac{{{y^2}}}{{{{16}^2}}} = 1\)

Phương trình nào dưới đây là phương trình chính tắc của đường parabol?

A. \({y^2} = \frac{x}{{10}}\)            

B. \({y^2} = \frac{{ - x}}{{10}}\) 

C. \({x^2} = \frac{y}{{10}}\)             

D. \({x^2} = \frac{{ - y}}{{10}}\)

Đường elip \(\frac{{{x^2}}}{{40}} + \frac{{{y^2}}}{{36}} = 1\) có hai tiêu điểm là:

A. F₁(-2 ; 0),  F₂ (2 ; 0)          

B. F₁(-4 ; 0),  F₂(4 ; 0)

C. F₁(0 ; -2),  F₂(0 ; 2)                  

D. F₁(0 ; -4),  F₂ (0 ; 4)

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(-3 ; -1), B(3 ; 5), C(3 ; -4). Gọi G, H, I lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC.

a) Lập phương trình các đường thẳng AB, BC, AC

b) Tìm toạ độ các điểm G, H, I

c) Tính diện tích tam giác ABC

Trong mặt phẳng toạ độ Oxy, cho hai điểm F₁(−4 ; 0) và F₂(4 ; 0).

a) Lập phương trình đường tròn có đường kính là F₁F₂

b) Tập hợp các điểm M trong mặt phẳng toạ độ thoả mãn MF₁ + MF₂ = 12 là một đường conic (E). Cho biết (E) là đường conic nào và viết phương trình chính tắc của (E)

c) Tập hợp các điểm M trong mặt phẳng toạ độ thoả mãn |MF₁ – MF₂| = 4 là một đường conic (H). Cho biết (H) là đường conic nào và viết phương trình chính tắc của (H)

Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(−1 ; −2), đường trung tuyến kẻ từ B và đường cao kẻ từ C lần lượt có phương trình là 5x + y – 9 = 0 và x + 3y − 5 = 0. Tìm toạ độ của hai điểm B và C.

Trong mặt phẳng toạ độ Oxy, cho hai điểm A(1 ; 0) và B(0 ; 3). Tìm tập hợp các điểm M thỏa mãn MA = 2MB.