Bài tập 12 trang 71 SGK Hình học 10 NC
Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau.
a) Chứng minh rằng AB2+CD2 không đổi.
b) Chứng minh rằng PA2+PB2+PC2+PD2 không phụ thuộc vào vị trí của điểm P.
Hướng dẫn giải chi tiết
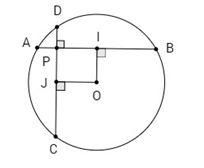
a) Gọi I, J lần lượt là trung điểm của AB, CD.
Ta có OI⊥AB; OJ⊥CD
Suy ra OIPJ là hình chữ nhật. Ta có:
\(\begin{array}{l}
A{B^2} + C{D^2} = 4\left( {A{I^2} + C{J^2}} \right)\\
= 4\left( {O{A^2} - O{I^2} + C{O^2} - J{O^2}} \right)
\end{array}\)
\( = 4\left( {2{R^2} - O{P^2}} \right)\) (không đổi do cố định)
b) Ta có:
\(\begin{array}{*{20}{l}}
{P{A^2} + P{B^2} + P{C^2} + P{D^2}}\\
\begin{array}{l}
= {\left( {\overrightarrow {PA} - \overrightarrow {PB} } \right)^2} + {\left( {\overrightarrow {PC} - \overrightarrow {PD} } \right)^2}\\
+ 2.\overrightarrow {PA} .\overrightarrow {PB} + 2\overrightarrow {PC} .\overrightarrow {PD}
\end{array}\\
{ = A{B^2} + C{D^2} + 4\left( {P{O^2} - {R^2}} \right)}\\
{ = 4\left( {2{R^2} - O{P^2}} \right) + 4\left( {P{O^2} - {R^2}} \right) = 4{R^2}}
\end{array}\)
Vậy \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P.
-- Mod Toán 10 HỌC247
-


Bài 2.27 trang 92 sách bài tập Hình học 10
bởi Thụy Mây
 06/11/2018
Bài 2.27 (SBT trang 92)
06/11/2018
Bài 2.27 (SBT trang 92)Trong mặt phẳng Oxy cho hai điểm \(A\left(5;5\right);B\left(3;-2\right)\). Một điểm M di động trên trục hoành Ox. Tìm giá trị nhỏ nhất của \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|\)
Theo dõi (0) 1 Trả lời -


Bài 2.26 trang 92 sách bài tập Hình học 10
bởi Trịnh Lan Trinh
 07/11/2018
Bài 2.26 (SBT trang 92)
07/11/2018
Bài 2.26 (SBT trang 92)Trong mặt phẳng Oxy cho 3 điểm \(A\left(-1;-1\right);B\left(3;1\right);C\left(6;0\right)\) ?
a) Chứng minh ba điểm A, B, C không thẳng hàng
b) Tính góc B của tam giác ABC
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 10 trang 71 SGK Hình học 10 NC
Bài tập 11 trang 71 SGK Hình học 10 NC
Bài tập 1 trang 71 SGK Hình học 10 NC
Bài tập 2 trang 71 SGK Hình học 10 NC
Bài tập 3 trang 71 SGK Hình học 10 NC
Bài tập 4 trang 71 SGK Hình học 10 NC
Bài tập 5 trang 72 SGK Hình học 10 NC
Bài tập 6 trang 72 SGK Hình học 10 NC
Bài tập 7 trang 72 SGK Hình học 10 NC
Bài tập 8 trang 72 SGK Hình học 10 NC
Bài tập 9 trang 72 SGK Hình học 10 NC
Bài tập 10 trang 72 SGK Hình học 10 NC
Bài tập 11 trang 73 SGK Hình học 10 NC
Bài tập 12 trang 73 SGK Hình học 10 NC
Bài tập 13 trang 73 SGK Hình học 10 NC
Bài tập 14 trang 73 SGK Hình học 10 NC





