Nß╗Öi dung b├Āi giß║Żng C├Īc ph├®p to├Īn tr├¬n tß║Łp hß╗Żp m├┤n To├Īn lß╗øp 10 chŲ░ŲĪng tr├¼nh Ch├ón trß╗Øi s├Īng tß║Īo ─æŲ░ß╗Żc HOC247 bi├¬n soß║Īn v├Ā tß╗Ģng hß╗Żp giß╗øi thiß╗ću ─æß║┐n c├Īc em hß╗Źc sinh, gi├║p c├Īc em t├¼m hiß╗āu vß╗ü Hß╗Żp v├Ā giao cß╗¦a c├Īc tß║Łp hß╗Żp, Hiß╗ću cß╗¦a hai tß║Łp hß╗Żp, phß║¦n b├╣ cß╗¦a tß║Łp con. ─Éß╗ā ─æi s├óu v├Āo t├¼m hiß╗āu v├Ā nghi├¬n cß╗®u nß╗Öi dung v├Āi hß╗Źc, mß╗Øi c├Īc em c├╣ng tham khß║Żo nß╗Öi dung chi tiß║┐t trong b├Āi giß║Żng sau ─æ├óy.
T├│m tß║»t l├Į thuyß║┐t
1.1. Hß╗Żp v├Ā giao cß╗¦a c├Īc tß║Łp hß╗Żp
|
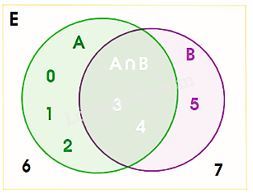
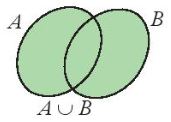
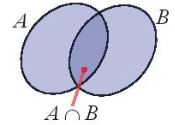
Cho hai tß║Łp hß╗Żp A v├Ā B. - Tß║Łp hß╗Żp c├Īc phß║¦n tß╗Ł thuß╗Öc A hoß║Ęc thuß╗Öc B gß╗Źi l├Ā hß╗Żp cß╗¦a hai tß║Łp hß╗Żp A v├Ā B, k├Ł hiß╗ću \(A \cup B\). \(A \cup B = {\rm{\{ }}x|x \in A\) hoß║Ęc \(x \in B{\rm{\} }}\) - Tß║Łp hß╗Żp c├Īc phß║¦n tß╗Ł thuß╗Öc cß║Ż hai tß║Łp hß╗Żp A v├Ā B gß╗Źi l├Ā giao cß╗¦a hai tß║Łp hß╗Żp A v├Ā B, k├Ł hiß╗ću \(A \cap B\). \(A \cap B = {\rm{\{ }}x|x \in A\) v├Ā \(x \in B{\rm{\} }}\) |
|---|
V├Ł dß╗ź: X├Īc ─æß╗ŗnh \(A \cup B\) v├Ā \(A \cap B\) trong mß╗Śi trŲ░ß╗Øng hß╗Żp sau:
a) A= {2; 3; 5; 7}, B={1; 3, 5; 15};
b) \(A = \left\{ {x \in R|x(x + 2) = 0} \right\},B = \left\{ {x \in R|{x^2} + 2 = 0} \right\}\)
c) A l├Ā tß║Łp hß╗Żp c├Īc h├¼nh b├¼nh h├Ānh, B l├Ā tß║Łp hß╗Żp c├Īc h├¼nh thoi.
Giß║Żi
a) 4\(A \cup B\) = (1;2;3;5; 7; 15), \(A \cap B\) = (3; 5}
b) PhŲ░ŲĪng tr├¼nh x(x + 2) = 0 c├│ hai nghiß╗ćm l├Ā 0 v├Ā -2. n├¬n A = {-2; 0}
PhŲ░ŲĪng tr├¼nh \({x^2} + 2 = 0\) v├┤ nghiß╗ćm, n├¬n B = ├ś
Từ đó \(A \cup B = A \cup \emptyset {\rm{ }} = A = \left\{ { - 2;0} \right\},A \cap B = A \cap {\rm{ }}\emptyset {\rm{ }} = {\rm{ }}\emptyset {\rm{ }}\)
e) V├¼ mß╗Śi h├¼nh thoi c┼®ng l├Ā h├¼nh b├¼nh h├Ānh n├¬n \(B \subset A\). Tß╗½ ─æ├│, \(A \cup B = A,A \cap B = B\)
Nhß║Łn x├®t:
- Nß║┐u A v├Ā B l├Ā hai tß║Łp hß╗Żp hß╗»u hß║Īn th├¼ \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)\)
- ─Éß║Ęc biß╗ćt, nß║┐u A v├Ā B kh├┤ng c├│ phß║¦n tß╗Ł chung, tß╗®c \(A \cap B = \emptyset \) \) th├¼ \(n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right)\)
1.2. Hiß╗ću cß╗¦a hai tß║Łp hß╗Żp, phß║¦n b├╣ cß╗¦a tß║Łp con
|
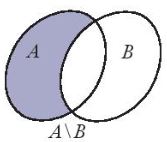
Cho hai tß║Łp hß╗Żp A v├Ā B. - T├óp hß╗Żp c├Īc phß║¦n tß╗Ł thuß╗Öc A nhŲ░ng kh├┤ng thuß╗Öc B gß╗Źi l├Ā liß╗ću cß╗¦a A v├Ā B, k├Ł hiß╗ću \(A\backslash B\) \(A\backslash B = {\rm{\{ }}x|x \in A\) v├Ā \(x \notin B{\rm{\} }}\). - Nß║┐u A l├Ā tß║Łp con cß╗¦a E th├¼ hiß╗ću \(E\backslash A\) gß╗Źi l├Ā ph├ón b├╣ cß╗¦a A trong E, k├Ł hiß╗ću \({C_E}A\). |
|---|
V├Ł dß╗ź: Cho E = {x \(\in\) N | x < 10}, A = {0; 2' 4; 6; 8}, B = {0; 3; 6; 9}
X├Īc ─æß╗ŗnh c├Īc tß║Łp hß╗Żp \(A\backslash B,B\backslash A,{C_E}A,{C_E}B\).
Giß║Żi
Ta c├│: \(A\backslash B = \left\{ {2;4;8} \right\},B\backslash A = \left\{ {3;9} \right\},{C_E}A = \left\{ {1;3;5;7;9} \right\},{C_E}B = \left\{ {1;2;4;5;7;8} \right\}\)
Ch├║ ├Į: Trong c├Īc chŲ░ŲĪng sau, ─æß╗ā t├¼m c├Īc tß║Łp hß╗Żp l├Ā hß╗Żp, giao, hiß╗ću, phß║¦n b├╣ cß╗¦a nhß╗»ng tß║Łp con cß╗¦a tß║Łp sß╗æ thß╗▒c, ta thŲ░ß╗Øng vß║Į sŲĪ ─æß╗ō tr├¬n trß╗źc sß╗æ.
B├Āi tß║Łp minh hß╗Źa
Câu 1: Cho \(A = \{ (x;y)|x,y \in \mathbb{R},3x - y = 9\} \), \(B = \{ (x;y)|\;x,y \in \mathbb{R},x - y = 1\} \)
H├Ży x├Īc ─æß╗ŗnh \(A \cap B\).
HŲ░ß╗øng dß║½n giß║Żi
\(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},3x - y = 9,x - y = 1\} \)
Tß╗®c l├Ā \(A \cap B\)l├Ā tß║Łp hß╗Żp c├Īc cß║Ęp sß╗æ (x;y) thß╗Åa m├Żn hß╗ć phŲ░ŲĪng tr├¼nh: \(\left\{ \begin{array}{l}3x - y = 9\\x - y = 1\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}y = 3x - 9\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 3x - 9\\y = x - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2x = 8\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right.\end{array}\)
Vß║Ły \(A \cap B = \{ (4;3)\} .\)
C├óu 2: Cho tß║Łp hß╗Żp \(E = \{ x \in \mathbb{N}|x < 8\} ,A = \{ 0;1;2;3;4\} ,B = \{ 3;4;5\} \)
X├Īc ─æß╗ŗnh c├Īc tß║Łp hß╗Żp sau ─æ├óy:
a) A\B, B\A v├Ā \((A\backslash B) \cap {\rm{(}}B\backslash A)\)
b) \({C_E}(A \cap B)\) v├Ā \(({C_E}A) \cap ({C_E}B)\)
c) \({C_E}(A \cup B)\) v├Ā \(({C_E}A) \cup ({C_E}B)\)
HŲ░ß╗øng dß║½n giß║Żi
\(E = \{ x \in \mathbb{N}|x < 8\} = \{ 0;1;2;3;4;5;6;7\} \)
a) Ta c├│: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \)
b) Ta c├│: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \)
c) Ta c├│: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)
Luyß╗ćn tß║Łp B├Āi 3 ChŲ░ŲĪng 1 To├Īn 10 CTST
Qua b├Āi giß║Żng C├Īc ph├®p to├Īn tr├¬n tß║Łp hß╗Żp n├Āy gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc c├Īc nß╗Öi dung nhŲ░ sau:
- Nß║»m vß╗»ng c├Īc kh├Īi niß╗ćm hß╗Żp, giao, hiß╗ću, phß║¦n b├╣ cß╗¦a hai tß║Łp hß╗Żp.
- Biß║┐t c├Īch x├Īc ─æß╗ŗnh hß╗Żp, giao, hiß╗ću, phß║¦n b├╣ cß╗¦a hai tß║Łp hß╗Żp.
3.1. B├Āi tß║Łp trß║»c nghiß╗ćm B├Āi 3 ChŲ░ŲĪng 1 To├Īn 10 CTST
─Éß╗ā c┼®ng cß╗æ b├Āi hß╗Źc xin mß╗Øi c├Īc em c┼®ng l├Ām B├Āi kiß╗ām tra Trß║»c nghiß╗ćm To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 1 B├Āi 3 ─æß╗ā kiß╗ām tra xem m├¼nh ─æ├Ż nß║»m ─æŲ░ß╗Żc nß╗Öi dung b├Āi hß╗Źc hay chŲ░a.
-
- A. Tß║Łp hß╗Żp A c├│ 8 phß║¦n tß╗Ł.
- B. Tß║Łp hß╗Żp B c├│ 6 phß║¦n tß╗Ł.
- C. Tß║Łp (A Ōł¬ B) c├│ 14 phß║¦n tß╗Ł.
- D. Tß║Łp hß╗Żp (B \ A) c├│ 2 phß║¦n tß╗Ł.
-
- A. A = {0; 1; 2; 3; 4; 6; 9; 10}.
- B. A = {0; 1; 2; 3; 4; 3; -2}.
- C. B = {0; 1; 2; 3; 4; -3; -2}.
- D. B = {0; 1; 2; 3; 4; -3; -2; 6; 9; 10}.
-
- A. 1
- B. 2
- C. 3
- D. Vô số
C├óu 4-10: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c v├Ā nß║»m vß╗»ng hŲĪn vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2. B├Āi tß║Łp SGK B├Āi 3 ChŲ░ŲĪng 1 To├Īn 10 CTST
B├¬n cß║Īnh ─æ├│ c├Īc em c├│ thß╗ā xem phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo ChŲ░ŲĪng 1 B├Āi 3 ─æß╗ā gi├║p c├Īc em nß║»m vß╗»ng b├Āi hß╗Źc v├Ā c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp.
Hoß║Īt ─æß╗Öng khß╗¤i ─æß╗Öng trang 21 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 1 trang 21 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Thß╗▒c h├Ānh 1 trang 23 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Thß╗▒c h├Ānh 2 trang 23 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Vß║Łn dß╗źng trang 23 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Hoß║Īt ─æß╗Öng kh├Īm ph├Ī 2 trang 23 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Thß╗▒c h├Ānh 3 trang 24 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Thß╗▒c h├Ānh 4 trang 25 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 1 trang 25 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 2 trang 25 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 3 trang 25 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 4 trang 25 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 5 trang 25 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 6 trang 25 SGK To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 1 trang 16 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 2 trang 16 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 3 trang 16 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 4 trang 17 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 5 trang 17 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 6 trang 17 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 7 trang 17 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 8 trang 17 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 9 trang 17 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 10 trang 17 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Giß║Żi b├Āi 11 trang 17 SBT To├Īn 10 Ch├ón trß╗Øi s├Īng tß║Īo tß║Łp 1 - CTST
Hß╗Åi ─æ├Īp B├Āi 3 ChŲ░ŲĪng 1 To├Īn 10 CTST
Trong qu├Ī tr├¼nh hß╗Źc tß║Łp nß║┐u c├│ thß║»c mß║»c hay cß║¦n trß╗Ż gi├║p g├¼ th├¼ c├Īc em h├Ży comment ß╗¤ mß╗źc Hß╗Åi ─æ├Īp, Cß╗Öng ─æß╗ōng To├Īn HOC247 sß║Į hß╗Ś trß╗Ż cho c├Īc em mß╗Öt c├Īch nhanh ch├│ng!
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt v├Ā lu├┤n ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp!
-- Mod To├Īn Hß╗Źc 10 Hß╗īC247


.JPG)