Thực hành 3 trang 24 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST

Hướng dẫn giải

Áp dụng kiến thức:

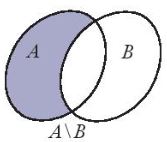
- Tâp hợp các phần tử thuộc A nhưng không thuộc B gọi là liệu của A và B, kí hiệu \(A\backslash B\)

\(A\backslash B = {\rm{\{ }}x|x \in A\) và \(x \notin B{\rm{\} }}\).

- Nếu A là tập con của E thì hiệu \(E\backslash A\) gọi là phân bù của A trong E, kí hiệu \({C_E}A\).

Lời giải chi tiết

a) Ta có A\B = {0; 1; 2} và B\A = {5}.

Khi đó (A\B) ∩ (B\A) = ∅.

b) Ta có: E = {0; 1; 2; 3; 4; 5; 6; 7}

Ta lại có: A ∩ B = {3; 4}

⇒ C_E(A ∩ B) = {0; 1; 2; 5; 6; 7}.

Ta có: C_EA = {5; 6; 7} và C_EB = {0; 1; 2; 6; 7}.

⇒ (C_EA) ∪ (C_EB) = {0; 1; 2; 5; 6; 7}.

c) Ta lại có: A ∪ B = {0; 1; 2; 3; 4; 5}.

⇒ C_E(A∪ B) = {6; 7}.

Ta có: C_EA = {5; 6; 7} và C_EB = {0; 1; 2; 6; 7}.

⇒ (C_EA) ∩ (C_EB) = {6; 7}.

-- Mod Toán 10 HỌC247