Ôn tập Hình học 12 Chương 2 Mặt Nón, Mặt Trụ, Mặt Cầu

Đề cương Ôn tập Hình học 12 Chương 2

A. Tóm tắt lý thuyết 

• Mặt nón, hình nón, khối nón.
• Mặt trụ, hình trụ, khối trụ.
• Mặt cầu, khối cầu, vị trí tương đối giữa mặt cầu với đường thẳng, mặt phẳng.

a) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

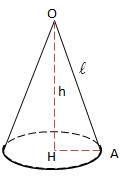
Cho hình nón có đường sinh \(l\), bán kính đáy \(R\), chiều cao \(h\), ta có các công thức sau:

• Thể tích khối nón: \(V_{Khoi \, \, non}=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h\).
• Diện tích xung quanh hình nón: \(S_{xq}=\pi Rl\).
• Diện tích toàn phần hình nón: \(S_{tp}=\pi Rl+\pi R^{2}\).

b) Các công thức tính toán liên quan đển hình trụ, khối trụ

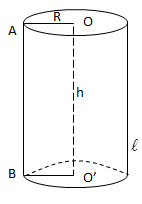
• Thể tích khối trụ: \(V=\pi .R^2.h\) (=Sđáy.h).
• Diện tích xung quanh hình trụ: \(S_{xq}=2\pi .R.h\).
• Diện tích toàn phân hình trụ: \(S_{tp}=2\pi .R.h+2\pi R^2\).

Trong đó:

• R: bán kính đáy.
• h: chiều cao (k/c giữa hai đáy = OO').​

c) Công thức tính toán liên qua đến mặt cầu, khối cầu

• Công thức tính thể tích khối cầu bán kính R: \(V=\frac{4}{3}\pi .R^3\).
• Công thức tính diện tích mặt cầu bán kính R: \(S = 4\pi {R^2}.\)

a) Mặt cầu ngoại tiếp hình chóp

• Hình chóp có một mặt cầu ngoại tiếp khi và chỉ khi đáy của hình chóp là đa giác nội tiếp.
• Cách xác định tâm mặt cầu ngoại tiếp hình chóp: nếu hình chóp có mặt cầu ngoại tiếp thì tâm mặt cầu ngoại tiếp hình chóp chính là giao điểm của mặt phẳng trung trực của một cạnh bên và trục dường tròn ngoại tiếp đa giác đáy.

b) Mặt cầu ngoại tiếp lăng trụ

• Hình lăng trụ có một mặt cầu ngoại tiếp khi và chỉ khi lăng trụ đó là lăng trụ đứng có đáy là đa giác nội tiếp.
• Cách xác định tâm mặt cầu ngoại tiếp lăng trụ: nếu lăng trụ có mặt cầu ngoại tiếp thì tâm đường tròn ngoại tiếp lăng trụ đó chính là trung điểm của đoạn nối tâm 2 đường tròn ngoại tiếp hai đa giác đáy.

B. Bài tập minh họa

Bài 1: Cho tam giác ABC vuông tại A có AC=3a, AB=4a. Cho tam giác này quay quanh đường thẳng BC, tính thể tích V của khối tròn xoay thu được.

Hướng dẫn giải

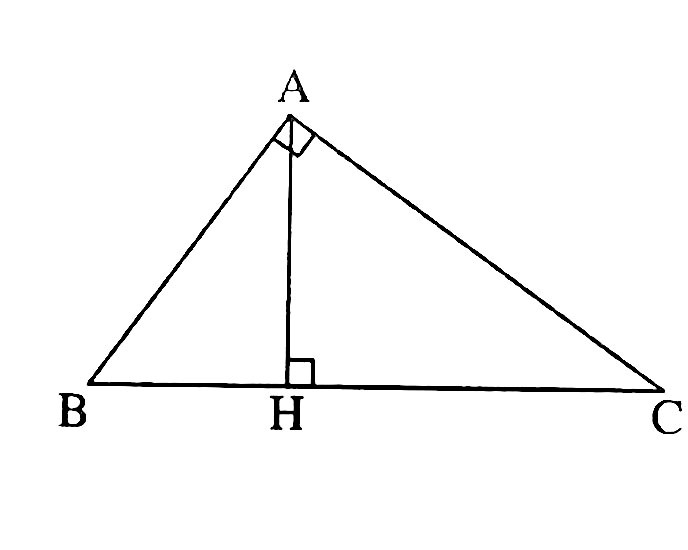
Kẻ đường cao AH của ∆ABC

Khi quay tam giác ABC quanh đường thẳng BC miền tam giác ABC sinh ra hai khối nón chung đáy có bán kính đáy là R = AH và chiều cao lần lượt là HB và HC.

Ta có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{16{a^2}}} + \frac{1}{{9{a^2}}} = \frac{{25}}{{144{a^2}}}.\)

Suy ra \(A{H^2} = \frac{{25}}{{144{a^2}}}.\)

Mặt khác: \(HB + HC = BC = \sqrt {A{B^2} + A{C^2}} = 5a.\)

Thể tích khối tròn xoay sinh ra là:

\(V = {V_1} + {V_2} = \frac{1}{3}\pi A{H^2}.\left( {HB + HC} \right) = \frac{1}{3}\pi .\frac{{144{a^2}}}{{25}}.5a = \frac{{144\pi {a^2}}}{{15}}.\)

Bài 2: Cho một cái bể nước hình hộp chữ nhật có ba kích thước 2m, 3m, 2m lần lượt là chiều dài, chiều rộng, chiều cao của lòng trong đựng nước của bể. Hàng ngày nước ở trong bể được lấy ra bởi một cái gáo hình trụ có chiều cao là 5 cm bà bán kính đường tròn đáy là 4 cm. Trung bình một ngày được múc ra 170 gáo nước để sử dụng (Biết mỗi lần múc là múc đầy gáo). Hỏi đến ngày thứ bao nhiêu bể sẽ hết nước?

Hướng dẫn giải

Thể tích nước được đựng đầy trong hình bể là là thể tích của hình hộp chữ nhật: \(V = 2.3.2 = 12\left( {{m^3}} \right).\)

Thể tích nước đựng đầy trong một gáo là: \({V_g} = \pi {4^2}.5 = 80\pi \left( {c{m^3}} \right) = \frac{\pi }{{12500}}\left( {{m^3}} \right).\)

Mội ngày bể được múc ra 170 gáo nước tức trong một ngày lượng được được lấy ra là: \({V_m} = 170.{V_g} = \frac{{17}}{{1250}}\pi \left( {{m^3}} \right)\).

Ta có: \(\frac{V}{{{V_m}}} = \frac{{12}}{{\frac{{17}}{{1250}}\pi }} \simeq 280,8616643\)

Vậy đến ngày thứ 281 bể sẽ hết nước.

Bài 3: Một quả bóng bàn và một chiếc chén hình trụ có cùng chiều cao. Người ta đặt quả bóng lên chiếc chén thấy phần ở ngoài của quả bóng có chiều cao bằng \(\frac{3}{4}\) chiều cao của nó. Tìm V1, V2 lần lượt là thể tích của quả bóng và chiếc chén. 

Hướng dẫn giải

Gọi chiều cao của chiếc chén hình trụ là 2h và bán kính đường tròn đáy của hình trụ là r.

Gọi O là tâm của quả bóng bàn, khi đó khoảng cách từ O đến mặt phẳng thiết diện bằng \(\frac{h}{2}\) 

Bán kính đường tròn đáy hình trụ là \(AI = \sqrt {O{A^2} - O{I^2}} = \frac{{h\sqrt 3 }}{2}.\)

Thể tích của quả bóng bàn là  \({V_1} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {h^3} = \frac{{4\pi {h^3}}}{3}.\)

Thể tích của chiếc chén là: \({V_2} = \pi {r^2}{h_c} = \pi {\left( {\frac{{h\sqrt 3 }}{2}} \right)^2}.2h = \frac{{3\pi {h^3}}}{2}.\) 

Bài 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC=2a. SA vuông góc (ABC) và \(SA = 2a\sqrt 2\). Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.

Hướng dẫn giải

Gọi M là trung điểm của BC.

Do ABC là tam giác vuông cân tại A nên: \(AB = AC = \frac{{BC}}{{\sqrt 2 }} = a\sqrt 2 ;AM = \frac{{BC}}{2} = a\)  

Dựng đường thẳng qua M song song với SA và cắt mặt phẳng trung trực của SA tại 0.

Khi đó O là tâm mặt cầu ngoại tiếp hình chóp.

Do ABCD là hình chữ nhật nên: \(OM=AE=a \sqrt 2.\)

Mặc khác: \(R = OA = \sqrt {O{M^2} + M{A^2}} = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {a^2}} = a\sqrt 3\)

Vậy thể tích khối cầu ngoại tiếp hình chóp là: \(V = \frac{4}{3}\pi {R^3} = 4\pi {a^3}\sqrt 3 .\)

Trắc nghiệm Hình học 12 Chương 2

• Trắc nghiệm Toán 12 Chương 2 Bài 1
• Trắc nghiệm Toán 12 Chương 2 Bài 2
• Trắc nghiệm ôn tập Chương 2 Toán 12 

Đề kiểm tra Hình học 12 Chương 2

Đề kiểm tra trắc nghiệm online Chương 2 Hình học 12 (Thi Online)

Phần này các em được làm trắc nghiệm online để kiểm tra năng lực và sau đó đối chiếu kết quả và xem đáp án chi tiết từng câu hỏi.

• 40 câu trắc nghiệm chuyên đề Mặt nón, mặt trụ và mặt cầu Hình học 12 năm học 2018 - 2019
• 40 câu trắc nghiệm ôn tập Chương 2 Hình học 12
• Đề kiểm tra 1 tiết Chương 2 Hình học 12 năm học 2018 - 2019
• Đề kiểm tra 1 tiết Chương 2 Hình học 12 Trường THPT Đào Duy Từ

Đề kiểm tra Chương 2 Hình học 12 (Tải File)

Phần này các em có thể xem online hoặc tải file đề thi về tham khảo gồm đầy đủ câu hỏi và đáp án làm bài.

• Chuyên đề Mặt Nón, Mặt Trụ, Mặt Cầu

Lý thuyết từng bài Chương 2 và hướng dẫn giải bài tập SGK

Lý thuyết các bài học  Hình học 12 Chương 2

• Hình học 12 Bài 1 Khái niệm về mặt tròn xoay
• Hình học 12 Bài 2 Mặt cầu
• Hình học 12 Ôn tập chương 2 Mặt nón, Mặt trụ, Mặt cầu

Hướng dẫn giải bài tập Toán 12 Chương 2

• Giải bài tập Toán 12 Chương 2 Bài 1
• Giải bài tập Toán 12 Chương 2 Bài 2
• Giải bài ôn tập Chương 2 Toán 12

Để xem nội dung đầy đủ, chi tiết, các em đăng nhập vào tài khoản trên trang Hoc247.net. Trên mỗi tài liệu, Hoc247 đều hỗ trợ chức năng chia sẻ lên Facebook để giới thiệu bạn bè cùng vào học, tích lũy thêm điểm HP và có cơ hội nhận thêm nhiều phần quà có giá trị từ HỌC247! Chúc các em đạt kết quả thật cao.