Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC có đáy là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC), SA=a, AB=b, AC=c

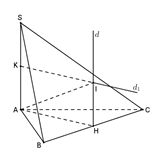
Gọi \(H,K\) lần lượt là trung điểm của \(BC\) và \(SA\).

Dựng đường thẳng \(d\) đi qua \(H\) và vuông góc với \(\left( {ABC} \right)\). Khi đó \(d{\rm{//}}SA\).

Trong mặt phẳng \(\left( {SAH} \right)\) dựng đường thẳng \({d_1}\) đi qua \(K\) và vuông góc với \(SA\).

Gọi \(d\) cắt \({d_1}\)  tại \(I\).

Ta có \(IA = IB = IC = IS\).

Khi đó mặt cầu đi qua các điểm \(A,B,C\) và \(S\) có tâm là \(I\) và bán kính là \(R = IA\).

Ta có \(AH = \frac{1}{2}BC = \frac{1}{2}\sqrt {A{B^2} + A{C^2}}  = \frac{{\sqrt {{b^2} + {c^2}} }}{2}\) và \(IH = \frac{1}{2}SA = \frac{a}{2}\).

Trong \(\Delta IAH\) có \(IA = \sqrt {A{H^2} + I{H^2}}  = \frac{1}{2}\sqrt {{a^2} + {b^2} + {c^2}}  = R\).