-
Câu hỏi:
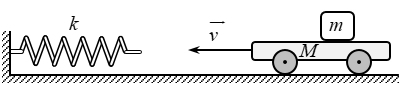
Ở hình bên, một lò xo nhẹ, có độ cứng k=4,8N/m được gắn một đầu cố định vào tường để lò xo nằm ngang. Một xe lăn, khối lượng M=0,2 kg và một vật nhỏ có khối lượng m=0,1 kg nằm yên trên xe, đang chuyển động dọc theo trục của lò xo với vận tốc v=20 cm/s, hướng đến lò xo. Hệ số ma sát nghỉ cực đại bằng hệ số ma sát trượt giữa vật nhỏ và xe là μ=0,04. Bỏ qua ma sát giữa xe và mặt sàn, coi xe đủ dài để vật không rời khỏi xe, lấy g=10 m/s2. Thời gian từ khi xe bắt đầu chạm lò xo đến khi lò xo nén cực đại gần nhất với giá trị nào sau đây?
- A. 0,345 s
- B. 0,361 s
- C. 0,513 s
- D. 0,242 s
Lời giải tham khảo:
Đáp án đúng: A
Để đơn giản, ta có thể chia quá trình chuyển động của xe thành các giai đoạn sau:
Giai đoạn 1: Hai vật dính vào nhau, dao động điều hòa quanh vị trí lò xo không biến dạng
- \({\omega _0} = \sqrt {\frac{k}{{M + m}}} = \sqrt {\frac{{\left( {4,8} \right)}}{{\left( {0,2 + 0,1} \right)}}} = 4\)rad/s → T1=π/2s.
- \(A = \frac{v}{{{\omega _0}}} = \frac{{\left( {20} \right)}}{{\left( 4 \right)}} = 5\)cm.
Trong hệ quy chiếu gắn với M, phương trình động lực học cho chuyển động của m
\({F_{qt}} - {F_{ms}} = ma'\)→ m trượt lên M khi a>0 và \({F_{ms}} = {\left( {{F_{ms}}} \right)_{max}}\)
→ \(x \ge \frac{{\mu g}}{{{\omega ^2}}} = \frac{{\left( {0,04} \right).\left( {10} \right)}}{{{{\left( 4 \right)}^2}}} = 2,5\)cm
→ Khi đi qua vị trí x=2,5cm, với vận tốc \(v = \frac{{\sqrt 3 }}{2}\omega A = \frac{{\sqrt 3 }}{2}\left( 4 \right)\left( 5 \right) = 10\sqrt 3 \)cm/s thì vật m sẽ trượt trên vật M, lực ma sát giữa hai vật là lực ma sát trượt.
Giai đoạn 2: Vật m trượt trên M, M dao động điều hòa chịu thêm tác dụng của ma sát.
- \(\omega = \sqrt {\frac{k}{M}} = \sqrt {\frac{{\left( {4,8} \right)}}{{\left( {0,2} \right)}}} = 2\sqrt 6 \)rad/s → \({T_2} = \frac{\pi }{{\sqrt 6 }}\).
- vị trí cân bằng mới cách vị trí lò xo không biến dạng một đoạn
\(\Delta {l_0} = \frac{{{F_{ms}}}}{k} = \frac{{\mu mg}}{k} = \frac{{\left( {0,04} \right).\left( {0,1} \right).\left( {10} \right)}}{{\left( {4,8} \right)}} = \frac{5}{6}\)cm.
- \(A' = \sqrt {{{x'}^2} + \left( {\frac{v}{\omega }} \right)} = \sqrt {{{\left( {2,5 - \frac{5}{6}} \right)}^2} + {{\left( {\frac{{10\sqrt 3 }}{{2\sqrt 6 }}} \right)}^2}} = \frac{{5\sqrt {22} }}{6}\)cm.
→ dừng lại lần đầu khi đến biên. Tổng thời gian chuyển động gồm:
\(t = \frac{{{T_1}}}{{12}} + \frac{{\arccos \left( {\frac{{x'}}{{A'}}} \right)}}{{{{360}^0}}}{T_2} = \frac{1}{{12}}\left( {\frac{\pi }{2}} \right) + \frac{{\left( {{{64,76}^0}} \right)}}{{{{360}^0}}}\left( {\frac{\pi }{{\sqrt 6 }}} \right) \approx 0,362\)s
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Theo thuyết lượng tử ánh sáng, ánh sáng được tạo thành bởi
- Vật dao động điều hòa với
- Trong máy quang phổ lăng kính, bộ phận
- Trong sóng cơ học
- Trong máy phát thanh đơn giản, mạch dùng để
- Trên một sợi dây đàn hồi, chiều dài l
- Một âm cơ học có tần số 12 Hz
- Dòng điện xoay chiều có biểu thức cường độ
- Trong các tia phóng xạ sau
- Máy biến áp sẽ không
- Kích thích một khối khí
- Mạch chọn sóng của một máy thu thanh
- Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở và tụ điện
- Biết năng lượng liên kết
- Theo mẫu nguyên tử Bo
- Một điện tích điểm q đặt tại điểm O
- Sóng truyền trên một sợi dây có
- Điện từ trường có thể
- Công tơ điện được sử dụng
- Một con lắc đơn dao động nhỏ
- Khi thực hiện thí nghiệm đo bước sóng
- Biết giới hạn quang điện của nhôm là
- Cho mạch điện như hình vẽ sau
- Dao động của một vật
- Mắt của một người bị tật
- Tiến hành thí nghiệm Y‒ âng về
- M là một điểm trong chân không có sóng điện từ truyền qua. Thành phần điện trường tại M
- Trong một môi trường đồng nhất
- Một sóng cơ hình sin lan truyền
- Một khung dây dẫn hình chữ nhật
- Một máy phát điện xoay chiều 3 pha
- Một con lắc lò xo treo thẳng đứng được kích thích cho dao động điều hòa
- Điện năng được truyền tải từ nơi phát
- Bắn hạt α vào hạt nhân nhôm Al đang đứng yên
- Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch AB
- Một con lắc đơn dao động nhỏ với chu kì 2,00 s.
- Thí nghiệm Y ‒ âng về giao thoa ánh sáng với
- Ở hình bên, một lò xo nhẹ
- Ở mặt chất lỏng, tại hai điểm A và B
- Một vật thực hiện đồng thời ba dao động