-
Câu hỏi:
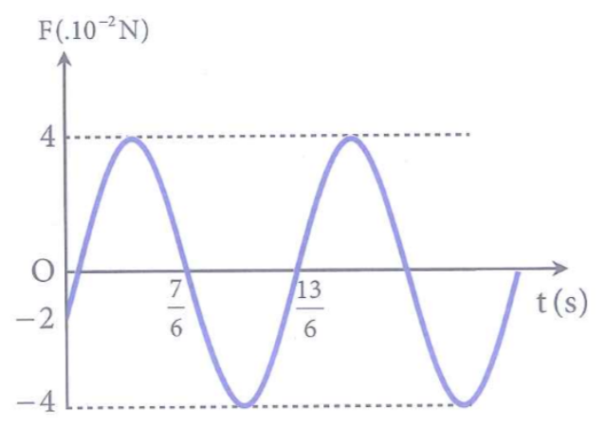
Một con lắc lò xo gồm một vật có khối lượng m = 100g gắn vào lò xo có độ cứng k, dao động điều hòa theo phương trình có dạng \(x = A\cos \left( {\omega t + \varphi } \right)\). Biết đồ thị lực kéo về theo thời gian F(t) như hình vẽ. Phương trình dao động của vật là
- A. \(x = 2\cos \left( {\pi t + \frac{\pi }{3}} \right)cm.\)
- B. \(x = 4\cos \left( {2\pi t + \frac{\pi }{3}} \right)cm.\)
- C. \(x = 2\cos \left( {2\pi t + \frac{\pi }{3}} \right)cm.\)
- D. \(x = 4\cos \left( {\pi t + \frac{\pi }{3}} \right)cm.\)
Lời giải tham khảo:
Đáp án đúng: D
Từ đồ thị ta có
\(\begin{array}{*{20}{l}}
{\Delta t = \frac{{13}}{6} - \frac{7}{6} = 1\left( s \right) = \frac{T}{2}}\\
{ \Rightarrow T = 2\left( s \right) \Rightarrow \omega = \frac{{2\pi }}{T} = \pi \left( {rad{\rm{ /}}s} \right)}\\
{{F_{kv\max }} = m{\omega ^2}A = 0,1{\pi ^2}A = {{4.10}^{ - 2}}\left( N \right) \Rightarrow A = 4\left( {cm} \right)}\\
{t = 0:{F_{kv}} = - m{\omega ^2}A = - {{2.10}^{ - 2}} \Rightarrow x = 2\left( {cm} \right)}
\end{array}\)F tăng => x giảm => vật đang chuyển động về vị trí cân bằng
\( \Rightarrow v < 0 \Rightarrow \varphi > 0 \Rightarrow \varphi = \arccos \frac{x}{A} = \arccos \frac{2}{4} = \frac{\pi }{3}\left( {rad} \right)\)
Vậy phương trình dao động của vật là:
\(x = 4\cos \left( {\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Thứ tự nào sau đây của các ánh sáng đơn sắc ứng với tần số tăng dần?
- Chọn câu đúng. Trong máy phát điện thì:
- Chọn câu đúng. Tia Rơn-ghen (tia X) có:
- Chọn câu đúng. Trong hạt nhân nguyên tử
- Chọn câu đúng nhất. Gọi k là hệ số nhân nơtron.
- Chọn công thức đúng. Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần
- Khi nói về sóng siêu âm, phát biểu nào sau đây sai?
- Con lắc đơn DĐĐH với pt: \(s = \cos \left( {2t + 0,69} \right)dm\)
- 1 người quan sát sóng trên mặt hồ thấy khoảng cách giữa 2 ngọn sóng là 1m
- 1 dòng điện XC có \(i = 4\cos \left( {100\pi t} \right)\left( A \right)\)
- Bức xạ có bước sóng trong khoảng từ \({3.10^{ - 9}}m - {3.10^{ - 7}}m\) là
- Sóng âm tần và sóng cao tần trong phát sóng vô tuyến có đặc điểm nào?
- Đối với các dụng cụ tiêu thụ điện như quạt, tủ lạnh, động cơ điện
- Hãy xác định trạng thái kích thích cao nhất của các nguyên tử hiđrô
- Một đèn laze có Pphát sáng 1 W phát ánh sáng đơn sắc có bước sóng 0,7μm.
- Một điện tích điểm q=1μC di chuyển từ điểm A đến điểm B trong điện trường
- Con lắc lò xo dao động, khối lượng vật nặng là 1 kg
- Một con lắc đơn dao động có chu kì 1,50(s).
- Trên sợi dây dài 1,2 m, hai đầu cố định, đang có sóng dừng với 5 nút sóng
- Cho đoạn mạch có một cuộn cảm thuần L và một điện trở R mắc nối tiếp.
- Cho phản ứng tổng hợp hạt nhân \({}_1^2D + {}_1^2D \to {}_Z^AZ + {}_0^1n\)
- Trong thí nghiệm giao thoa sóng, người ta tạo ra hai nguồn sóng A, B
- Một vật nhỏ thực hiện đồng thời hai dao động điều hòa cùng phương
- Biết các năng lượng liên kết của lưu huỳnh S32, crôm Cr52, urani U238
- Một electron chuyển động thẳng đều trong miền có cả từ trường đều
- Một miếng gốc hình tròn, bán kính 4cm. Ở tâm O, cắm thẳng góc một đinh OA.
- Cho mạch điện như hình vẽ, E = 12(V), r=1Ω;Đèn thuộc loại là một biến trở.
- Một con lắc lò xo gồm một vật có m = 100g gắn vào LX có độ cứng k
- Cho mạch RLC. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có U = 100V
- Cho hai máy biến áp, các cuộn dây sơ cấp có cùng số vòng dây
- Mạch dao động LC gồm 1 tụ điện và 1 cuộn dây thuần cảm đang có dao động
- Kết quả nào đúng? Trong thí nghiệm Y-âng, trên màn quan sát tại điểm M
- Chiếu ánh sáng trắng (có bước sóng λ biến đổi từ 400 nm tới 760 nm)
- Một mạch điện gồm một điện quang điện trở mắc nối tiếp với một bóng đèn Đ
- Urani sau nhiều lần phóng xạ α và ß- biến thành Pb.
- Một âm thoa có tần số f dao động riêng 850 Hz đặt sát miệng ống nghiệm
- Trong thí nghiệm giao thoa bằng khe Y-âng, người ta dùng kính lọc sắc
- Hai con lắc đơn có cùng chiều dài l, cùng khối lượng m
- Có hai nguồn sóng A, B cách nhau 20 cm dao động theo phương thẳng đứng
- Đoạn mạch AB gồm AM (chứa tụ điện C nối tiếp điện trở R) và đoạn mạch MB







