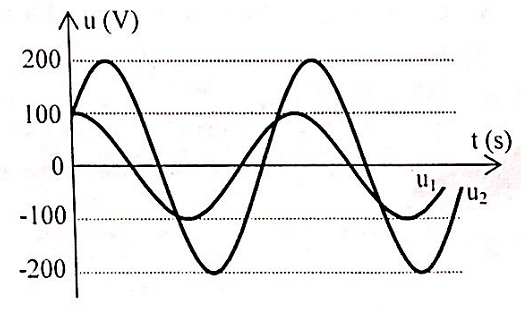
Mạch điện xoay chiều gồm cuộn dây thuần cảm L, đoạn mạch X và tụ điện C

+ Theo đề, ta có:

\({\omega ^2} = \frac{1}{{{L_0}{C_0}}} \Leftrightarrow \omega {L_0} = \frac{1}{{\omega {C_0}}} \Leftrightarrow {Z_L} = {Z_C}\) (1)

+ Từ đồ thị ta viết được biểu thức:

\(\left\{ \begin{array}{l}
{u_1} = 100\cos \omega t\left( V \right)\\
{u_2} = 200\cos \left( {\omega t - \frac{\pi }{3}} \right)\left( V \right)
\end{array} \right.\) 

+ Vì uL và uC ngược pha nên

\(\frac{{{u_L}}}{{{U_{0L}}}} =  - \frac{{{u_C}}}{{{U_{0C}}}} \Leftrightarrow \frac{{{u_L}}}{{{U_L}}} =  - \frac{{{u_C}}}{{{U_C}}}{u_L} =  - {u_C}\)  (2)

+ Lại có:

\(\left\{ \begin{array}{l}
{u_{LX}} = {u_L} + {u_X} = {u_1}\\
{u_{XC}} = {u_X} + {u_C} = {u_2}
\end{array} \right.\left\{ \begin{array}{l}
{u_1} = {u_L} + {u_X}\\
{u_2} = {u_X} - {u_L}
\end{array} \right. \Rightarrow {u_X} = \frac{{{u_1} + {u_2}}}{2}\) 

+ Theo đề, ta có:

\(\begin{array}{l}
{u_X} = \frac{{100 + 200\angle \frac{{ - \pi }}{3}}}{2} = 50\sqrt 7 \angle  - 0,71\\
 \Rightarrow {U_X} = \frac{{{U_{0X}}}}{{\sqrt 2 }} = \frac{{50\sqrt 7 }}{{\sqrt 2 }} = 25\sqrt {14} \left( V \right)
\end{array}\)