Với dạng bài tập này thường xuất hiện khoảng 2 - 3 câu trong 1 đề, tuy nhiên bài ra thường thì dễ và chủ yếu là tập trung vào kĩ năng xác định được loại đột biến NST:
1. Bài tập đột biến cấu trúc
Lưu ý: xác định dạng đột biến để suy ra hậu quả.
2. Bài tập đột biến số lượng
2.1. Đột biến lệch bội
Lưu ý: Khái niệm thể không, thê một, thể một kép...
2.2. Đột biến đa bội
Lưu ý:
- Cách viết sơ đồ lai và viết giao tử lưỡng bội của các cơ thể lai.
- Tập trung vào các tỷ lệ: 11 : 1; 35 : 1; 18 : 8 : 8 : 1.
Đôi khi cũng gặp 1 vài bài toán di truyền mang đột biến đa bội lẻ:
Ví dụ: AAa thì sinh ra giao tử như thế nào?
Chúng ta chỉ cần dùng sơ đồ tam giác:
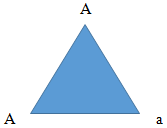
Viết tên 3 đỉnh và 3 cạnh của tam giác là ta sẽ có tỉ lệ các giao tử sinh ra bởi AAA: 1/6 AA : 2/6 Aa : 2/6 A : 1/6 a
 Playlist:
THPT QG Sinh học - Chuyên đề biến...
Playlist:
THPT QG Sinh học - Chuyên đề biến...
-
Video liên quan
-
Nội dung
-
Bài 1: Tìm khoảng đơn điệu của hàm số

Bài 1: Tìm khoảng đơn điệu của hàm số
Bài giảng sẽ giúp các em nắm được kiến thức cơ bản về cách tìm khoảng đơn điệu của hàm số như: Định nghĩa Điều kiện đủ để hàm số đơn điệu Các bước tìm khoảng đơn điệu của hàm số00:55:29 5364 TS. Phạm Sỹ Nam
-
Bài 2: Tìm tham số để hàm số đơn điệu trên một miền

Bài 2: Tìm tham số để hàm số đơn điệu trên một miền
Bài giảng sẽ giúp các em nắm được kiến thức cơ bản về cách tìm tham số để hàm số đơn điệu trên một miền như: Công thức tính. Điều kiện đủ để hàm số đơn điệu trên một miền.00:28:42 1092 TS. Phạm Sỹ Nam
-
Bài 3: Ứng dụng tính đơn điệu giải phương trình

Bài 3: Ứng dụng tính đơn điệu giải phương trình
Bài giảng sẽ giúp các em nắm kỹ hơn về lý thuyết và một số ví dụ cụ thể về ứng dụng tính đơn điệu giải phương trình.00:32:49 1101 TS. Phạm Sỹ Nam
-
Bài 4: Ứng dụng tính đơn điệu giải bất phương trình

Bài 4: Ứng dụng tính đơn điệu giải bất phương trình
Bài giảng Ứng dụng tính đơn điệu giải bất phương trình sẽ giúp các em nắm được lý thuyết và bài tập để các em củng cố kiến thức.00:32:29 891 TS. Phạm Sỹ Nam
-
Bài 5: Ứng dụng tính đơn điệu giải hệ phương trình

Bài 5: Ứng dụng tính đơn điệu giải hệ phương trình
Bài giảng Ứng dụng tính đơn điệu giải hệ phương trình sẽ giúp các em nắm kỹ hơn cách giải hệ phương trình, cách tìm tính nghịch biến, đồng biến về tính đơn điệu của hệ phương trình.00:29:14 968 TS. Phạm Sỹ Nam
-
Bài 6: Ứng dụng tính đơn điệu chứng minh bất đẳng thức

Bài 6: Ứng dụng tính đơn điệu chứng minh bất đẳng thức
Bài giảng ứng dụng tính đơn điệu chứng minh bất đẳng thức gồm có 2 phần nội dung chính: Lý thuyết Các ví dụ cụ thể nhằm giúp các em chứng minh được đồng biến và nghịch biến.00:43:58 1099 TS. Phạm Sỹ Nam
Chào tất cả các em! Thầy sẽ đi tiếp một nội dung của chuyên đề 3, hôm nay thầy sẽ hướng dẫn cho chúng ta phương pháp giải bài tập về đột biến NST.
Đối với phần đột biến NST các em cần chú ý:
A. Công thức và bài tập đột biến cấu trúc NST
1. Xác định loại giao tử tạo ra khi có rối loạn trong giảm phân:
Ví dụ: Aa giảm phân tạo giao tử
Ví dụ 2: AaBb
Ví dụ 3: Aa bị rối loạn gp1, giao tử?
⇒ Kết luận: Nếu có rối loạn trong giảm phân → tạo ra 2 loại giao tử: (n + 1) và (n - 1)
Ví dụ 4: Aa bị rối loạn gp2 → giao tử?
⇒ Kết luận: Nếu rối loạn gp2 → tạo ra 3 loại giao tử n; (n + 1); (n - 1)
* Có sự khác biệt giao tử (n + 1) do rối loạn giảm phân 1 và 2:
2. Xác định số giao tử của thể đa bội
Giả sử 1 gen có 2 alen A và a
+ Thể lưỡng bội ⇒ kiểu gen AA; Aa; aa
+ Thể tam bội ⇒ kiểu gen AAA; AAa; Aaa; aaa
+ Thể tứ bội ⇒ kiểu gen AAAA; AAAa; AAaa; Aaaa; aaaa
* Nếu thể lưỡng bội:
* Nếu thể tam bội:
- Sử dụng quy tắc tam giác
- Ví dụ 1: AAa
- Ví dụ 2: AAA
⇒ Thể tam bội giảm phân tạo ra 2 loại giao tử n và 2n
* Nếu thể tứ bội:
- Sử dụng quy tắc hình chữ nhật
Ví dụ:
\(\\ AAAa\xrightarrow[]{ \ gp \ } \frac{3}{6} \ \underline {AA}:\frac{3}{6} \ \underline{Aa} \\ \ (4n) \ \ \ \ \ \ \ \ \ \ \ \ \ (2n) \ \ \ \ (2n)\)
⇒ Thể tứ bội khi giảm phân tạo ra 1 loại giao tử: 2n
3. Xác định tỉ lệ đời con (kiểu hình, kiểu gen)
Ví dụ 1: P: ♂ Aa x ♀ AAA
Xác định tỉ lệ cá thể kiểu gen Aa đời con?
Giải:
P: ♂ Aa x ♀ AAA
GP: \(\frac{1}{2}A:\frac{1}{2}a\) \(\downarrow\) \(\frac{1}{2}A:\frac{1}{2}AA\)
F1: \(Aa = \frac{1}{2}A\) x \(\frac{1}{2}a=\frac{1}{4}\)
Ví dụ 2: P: ♂ Aa x ♀ AAAa
Xác định tỉ lệ kiểu hình F1?
Giải:
P: ♂ Aa x ♀ AAAa
GP: \(\frac{1}{2}A:\frac{1}{2}a\) \(\downarrow\) \(\frac{1}{2}AA:\frac{1}{2}Aa\)
F1: \(\frac{1}{4}AAA:\frac{1}{4}AAa:\frac{1}{4}AAa:\frac{1}{4}Aaa\)
⇒ F1: 100% trội
B. Công thức và bài tập đột biến số lượng NST
1. Cách viết giao tử của cá thể biến dị
Giả sử cá thể 2n có kiểu gen Aa trải qua giảm phân → tạo ra 2 loại giao tử A và a\(\begin{matrix} Aa\\ (2n) \end{matrix} \rightarrow AAaa \xrightarrow[ \ gp_{1} \ ]{ \ } \frac{AA}{aa} \left < \begin{matrix} AA \left < \begin{matrix} A (n) \\ a(n) \end{matrix} \right. \\ \\ \begin{matrix} aa \\ gp_{2} \end{matrix} \left < \begin{matrix} a (n) \\ a(n) \end{matrix} \right. \end{matrix} \right.\)
* Nếu quá trình giảm phân 1 có rối loạn (NST nhân đôi nhưng không phân li)
Vậy khi xảy ra rối loạn gp1 → 2 loại giao tử: \(\left\{\begin{matrix} n+1 \\ n-1 \end{matrix}\right.\)
* Nếu quá trình giảm phân 2 xảy ra rối loạn:
Vậy khi xảy ra rối loạn gp2 → 3 loại giao tử \(\left\{\begin{matrix} n \ \ \ \ \ \\ n+1 \\ n-1 \end{matrix}\right.\)
2. Cách viết giao tử của thể tam bội và tứ bội
+ Cá thể 2n \(\xrightarrow[]{ \ gp \ }\) n
Ví dụ: \(\underset{(2n)}{Aa}\left < \begin{matrix} A \ (n)\\ a \ (n) \end{matrix} \right.\)
+ Cá thể 3n:
Ví dụ: \(AAa\xrightarrow[]{ \ gp \ } \frac{2}{6}A:\frac{1}{6}a:\frac{1}{6}AA:\frac{2}{6}Aa\)
(n) (n) (2n) (2n)
Vậy thể tam bội \(\xrightarrow[]{ \ gp \ }\) \(\left\{\begin{matrix} gt \ n \ \\ gt \ 2n \end{matrix}\right.\)
.PNG)
Ví dụ 2: AAA →
\(AAA\rightarrow \frac{3}{6}A:\frac{3}{6}AA\)
(n) (2n)
+ Cá thể 4n:
Ví dụ 1: AAAa \(\xrightarrow[]{ \ gp \ }\)
\(AAAa \xrightarrow[]{ \ gp \ }\frac{3}{6}Aa:\frac{3}{6}AA\)
(2n) (2n)
Vậy thể tứ bội (4n) \(\xrightarrow[]{ \ gp \ }\) giao tử 2n
Ví dụ 2: AAaa \(\xrightarrow[]{ \ gp \ }\)
\(AAaa \xrightarrow[]{ \ gp \ }\frac{1}{6}AA:\frac{4}{6}Aa:\frac{1}{6}aa\)
3. Cách viết sơ đồ lai
Ví dụ:
Cho P: ♀ Aa x ♂ AAa
GP: \(\frac{1}{2}A:\frac{1}{2}a\) \(\downarrow\) \(\frac{2}{6}A:\frac{1}{6}a:\frac{1}{6}AA:\frac{2}{6}Aa\)
F1: \(\frac{2}{12}AA:\frac{1}{12}Aa:\frac{1}{12}AAA:\frac{2}{12}AAa\)
\(\frac{2}{12}Aa:\frac{1}{12}aa:\frac{1}{12}AAa:\frac{2}{12}Aaa\)
\(TLKG: \frac{2}{12}AA:\frac{3}{12}Aa:\frac{1}{12}aa:\frac{1}{12}AAA:\frac{3}{12}AAa:\frac{2}{12}Aaa\)
\(TLKH: \ 11T:1L\)
Ví dụ 2: Cho phép lai P: ♀ AAa x ♂ Aaa
Biết A: đỏ > a: trắng và hạt phấn 2n không có khả năng thụ tinh. Xác định tỉ lệ kiểu hình đời con?
Giải:
4. Xác định tỉ lệ kiểu gen và kiểu hình đời con
Ví dụ: Cho P: AAaa x aa Biết A: cao > a thấp. Xác định:
a) Tỉ lệ cá thể có kiểu gen aaa?
b) Tỉ lệ kiểu hình cây thấp đời con? Cao?
Giải:
P: AAaa x aa
a) \(aaa = aa \times a = \frac{1}{6}\)
\(\frac{1}{6}\) \(1\)
b) \(Cao = 1-\frac{1}{6}=\frac{5}{6}\)






.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
(1).PNG)
(1).PNG)
.PNG)
.PNG)