Giải Toán 12 SGK nâng cao Chương 3 Bài 2 Phương trình mặt phẳng

Trong mỗi trường hợp sau, viết phương trình mặt phẳng:

a) Đi qua ba điểm M(2; 0; −1); N(1; −2; 3); P(0; 1; 2)

b) Đi qua hai điểm A(1; 1; −1); B(5; 2; 1) và song song với trục Oz ;

c) Đi qua điểm (3; 2; -1) và song song với mặt phẳng có phương trình x –5y + z = 0;

d) Đi qua hai điểm A(0 ; 1 ; 1), B(- 1 ; 0 ; 2) và vuông góc với mặt phẳng x – y + z – 1 = 0 ;

e) Đi qua điểm M(a ; b ; c) (với abc ≠ 0) và song song với một mặt phẳng toạ độ ;

g) Đi qua điểm G(1 ; 2 ; 3) và cắt các trục toạ độ tại các điểm A, B, C sao cho G là trọng tâm tam giác ABC ;

h) Đi qua điểm H(2 ; 1 ; 1) và cắt các trục toạ độ tại các điểm A, B, C sao cho H là trực tâm của tam giác ABC.

Hướng dẫn giải:

Câu a:

Ta có: \(\overrightarrow {MN}  = \left( { - 1; - 2;4} \right),{\mkern 1mu} {\kern 1pt} \overrightarrow {MP}  = \left( { - 2;1;3} \right)\)

\( \Rightarrow \left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( { - 10; - 5; - 5} \right) =  - 5\left( {2;1;1} \right)\)

Chọn vectơ pháp tuyến của mp(MNP) là \(\overrightarrow n  = (2;1;1)\). Mp(MNP) đi qua M(2; 0; −1) và có vectơ pháp tuyến \(\overrightarrow n  = (2;1;1)\) nên có phương trình là:

\(2(x - 2) + 1(y - 0) + 1(z + 1) = 0 \Leftrightarrow 2x + y + z - 3 = 0\)

Câu b:

Mp(P) đi qua A, B và song song với trục Oz có vectơ pháp tuyến \(\overrightarrow n \) vuông góc với \(\overrightarrow {AB}  = (4;1;2)\) và vuông góc với \(\vec k = \left( {0;0;1} \right)\) nên:

\(\overrightarrow n  = \left[ {\overrightarrow {AB} ,\overrightarrow k } \right] = \left( {\left| {\begin{array}{*{20}{c}}
1&2\\
0&1
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
2&4\\
1&0
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
4&1\\
0&0
\end{array}} \right|} \right) = \left( {1; - 4;0} \right)\)

(P) qua A(1;1;−1) và có vectơ pháp tuyến \(\overrightarrow n  = (1; - 4;0)\) nên (P) có phương trình:

\(1(x - 1) - 4(y - 1) + 0(z + 1) = 0 \Leftrightarrow x - 4y + 3 = 0\)

Câu c:

 Mặt phẳng (α): x − 5y + z = 0 có vectơ pháp tuyến \(\vec n = \left( {1; - 5;1} \right)\)

Mp(β) qua A(3; 2; −1) song song với mp(α) nên (β) có cùng vectơ pháp tuyến .

Do đó: \(\left( \beta  \right):(x - 3) - 5(y - 2) + (z + 1) = 0 \Leftrightarrow x - 5y + z + 8 = 0\)

Câu d:

Ta có: \(\overrightarrow {AB}  = ( - 1; - 1;1)\)

Mp(α): x − y + z + 1 = 0 có vectơ pháp tuyến \(\vec m = \left( {1; - 1;1} \right)\)

Mp(β) đi qua A, B và vuông góc với mp(α) nên vectơ pháp tuyến của (β) vuông góc với \(\overrightarrow {AB} \) và vuông góc với \(\overrightarrow m \) nên ta có thể chọn:

\(\overrightarrow n  = \left[ {\overrightarrow {AB} ;\overrightarrow m } \right] = (0;2;2)\)

Vậy (P): 2(y−1) + 2(z−1) = 0 <=> y + z − 2 = 0

Câu e:

Mặt phẳng đi qua M(a, b, c) song song với mp(Oxy) có vectơ pháp tuyến là \(\vec k = \left( {0;0;1} \right)\) nên có phương trình: 1(z − c) = 0 <=> z − c = 0

Tương tự mặt phẳng đi qua M(a, b, c) song song với mp(Oyz) có phương trình x – a = 0; mặt phẳng đi qua M(a, b, c) song song với mp(Oxz) có phương trình y – b = 0.

Câu g:

Giả sử A(a; 0; 0), B(0, b, 0), C(0, 0, c).

Vì G là trọng tâm của tam giác ABC nên \(\frac{{a + 0 + 0}}{3} = 1;\frac{{0 + b + 0}}{3} = 2;\frac{{0 + 0 + c}}{3} = 3 \Rightarrow a = 3;b = 6;c = 9\)

Vậy mp(ABC): \(\frac{x}{3} + \frac{y}{6} + \frac{z}{9} = 1\)

Câu h:

Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc nên H là trực tâm ΔABC khi và chỉ khi OH ⊥ mp(ABC).

Vậy mp(ABC) đi qua H va có vectơ pháp tuyến là \(\overrightarrow {OH}  = (2;1;1)\) nên có phương trình 

2(x−2) + (y−1) + (z−1) = 0 <=> 2x + y + z − 6 = 0

---

Xét vị trí tương đối của mỗi cặp mật phẳng cho bởi các phương trình sau:

a) x + 2y − z + 5 = 0 và 2x + 3y − 7z − 4 = 0
b) z − 2y + z − 3 = 0 và 2x − y + 4z − 2 = 0
c) x + y + z − 1 = 0 và 2x + 2y + 2z + 3 = 0.
d) 3x − 2y + 3z + 5 = 0 và 9x − 6y − 9z − 5 = 0
e) x − y + 2z − 4 = 0 và 10x − 10y + 20z − 40 = 0

Hướng dẫn giải:

Câu a:

Ta có 1 : 2 : (−1) ≠ 2 : 3 : (−7) nên hai mặt phẳng đã cho cắt nhau.

Câu b:

1 : (−2) : 1 ≠ 2 : (−1) : 4 nên hai mặt phẳng cắt nhau.

Câu c:

\(\frac{1}{2} = \frac{1}{2} = \frac{1}{2} \ne \frac{{ - 1}}{3}\) nên hai mặt phẳng song song.

Câu d:

 3 : (−2) : 3 ≠ 9 : (−6) : (−9) nên hai mặt phẳng cắt nhau.

Câu e:

\(\frac{1}{{10}} = \frac{{ - 1}}{{ - 10}} = \frac{2}{{20}} = \frac{{ - 4}}{{ - 40}}\) nên hai mặt phẳng trùng nhau

---

Xác định giá trị của m và n để mỗi cặp mặt phẳng sau đây song song:

a) 2x + ny + 2z + 3 = 0 và mx + 2y − 4z + 7 = 0
b) 2x + y + mz − 2 = 0 và x + ny + 2z + 8 = 0.

Hướng dẫn giải:

Câu a:

 Hai mặt phẳng đã cho song song với nhau khi và chỉ khi:

\(\frac{2}{m} = \frac{n}{2} = \frac{2}{{ - 4}} \ne \frac{3}{7} \Leftrightarrow \left\{ \begin{array}{l}
m =  - 4\\
n =  - 1
\end{array} \right.\)

Câu b:

Hai mặt phẳng đã cho song song với nhau khi và chỉ khi:

\(\frac{2}{1} = \frac{1}{n} = \frac{{2m}}{2} \ne \frac{{ - 2}}{8} \Leftrightarrow \left\{ \begin{array}{l}
m = 4\\
n = \frac{1}{2}
\end{array} \right.\)

---

Cho hai mặt phẳng có phương trình là 
2x − my + 3z − 6 + m = 0 và (m + 3)x− 2y + (5m + 1)z − 10 = 0

Với giá trị nào của m thì:

a) Hai mặt phẳng đó song song 

b) Hai mặt phẳng đó trùng nhau

c) Hai mặt phẳng đó cắt nhau 

Hướng dẫn giải:

Mặt phẳng 2x − my + 3z − 6 + m = 0 có vectơ pháp tuyến \(\overrightarrow {{n_1}}  = \left( {2; - m;3} \right)\)

Mặt phẳng (m + 3)x − 2y + (5m + 1)z − 10 = 0 có vectơ pháp tuyến \(\overrightarrow {{n_2}}  = \left( {m + 3; - 2;5m + 1} \right)\)

Ta có

\(\left[ {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right] = \overrightarrow 0  \Leftrightarrow \left\{ \begin{array}{l}
 - 5{m^2} - m + 6 = 0\\
 - 7m + 7 = 0\\
{m^2} + 3m - 4 = 0
\end{array} \right. \Leftrightarrow m = 1\)

Với m = 1 thì hai mặt phẳng có phương trình 2x − y + 3z − 5 = 0 và 4x − 2y + 6z − 10 = 0 nên chúng trùng nhau.

Câu a:

Không tồn tại m để hai mặt phẳng đó song song.

Câu b:

Với m = 1 thì hai mặt phẳng đó trùng nhau.

Câu c:

 Với m ≠ 1 thì hai mặt phẳng đó cắt nhau.

Câu d:

Hai mặt phẳng đó vuông góc với nhau khi và chỉ khi

\(\overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 0 \Leftrightarrow 2(m + 3) + 2m + 3(5m + 1) = 0 \Leftrightarrow m = \frac{{ - 9}}{{19}}\)

---

Tìm tập hợp các điểm cách đều hai mặt phẳng (α) và (α′) trong mỗi trường hợp sau:

\(\begin{array}{l}
a)(\alpha ):2x - y + 4z + 5 = 0,(\alpha \prime ):3x + 5y - z - 1 = 0\\
b)(\alpha ):2x + y - 2z - 1 = 0,(\alpha \prime ):6x - 3y + 2z - 2 = 0\\
c)(\alpha ):x + 2y + z - 1 = 0,(\alpha \prime ):x + 2y + z + 5 = 0
\end{array}\)

Hướng dẫn giải:

Câu a:

Điểm M(x,y,z) cách đều hai mặt phẳng đã cho khi và chỉ khi:

\(\begin{array}{l}
\frac{{|2x - y + 4z + 5|}}{{\sqrt {4 + 1 + 16} }} = \frac{{|3x + 5y - z - 1|}}{{\sqrt {9 + 25 + 1} }}\\
 \Leftrightarrow \sqrt 5 |2x - y + 4z + 5| = \sqrt 3 |3x + 5y - z - 1|\\
 \Leftrightarrow \sqrt 5 (2x - y + 4z + 5) =  \pm \sqrt 3 (3x + 5y - z - 1)
\end{array}\)

Vậy tập hợp các điểm M là hai mặt phẳng

\(\begin{array}{l}
(2\sqrt 5  - 3\sqrt 3 )x - (\sqrt 5  + 5\sqrt 3 )y + (4\sqrt 5  + \sqrt 3 )z + 5\sqrt 5  + \sqrt 3  = 0\\
(2\sqrt 5  + 3\sqrt 3 )x - (\sqrt 5  - 5\sqrt 3 )y + (4\sqrt 5  - \sqrt 3 )z + 5\sqrt 5  - \sqrt 3  = 0
\end{array}\)

Câu b:

Điểm M(x, y, z) cách đều hai mặt phẳng đã cho khi và chỉ khi:

\(\begin{array}{l}
\frac{{|2x + y - 2z - 1|}}{{\sqrt {4 + 1 + 4} }} = \frac{{|6x - 3y + 2z - 2|}}{{\sqrt {36 + 9 + 4} }}\\
 \Leftrightarrow \left[ \begin{array}{l}
7(2x + y - 2z - 1) = 3(6x - 3y + 2z - 2)\\
7(2x + y - 2z - 1) =  - 3(6x - 3y + 2z - 2)
\end{array} \right.\\
 \Leftrightarrow \left[ \begin{array}{l}
 - 4x + 16y - 20z - 1 = 0\\
32x - 2y - 8z - 13 = 0
\end{array} \right.
\end{array}\)

Tập hợp các điểm M là hai mặt phẳng có phương trình:

\(\begin{array}{l}
 - {\rm{ }}4x{\rm{ }} + {\rm{ }}16y - 20z - 1 = 0\\
 \Leftrightarrow 32x - 2y - 8z - 13 = 0
\end{array}\)

Câu c:

Điểm M(x, y, z) cách đều hai mặt phẳng đã cho khi và chỉ khi:

\(\begin{array}{l}
\frac{{|x + 2y + z - 1|}}{{\sqrt {1 + 4 + 1} }} = \frac{{|x + 2y + z + 5|}}{{\sqrt {1 + 4 + 1} }}\\
 \Leftrightarrow \left[ \begin{array}{l}
x + 2y + z - 1 = x + 2y + z + 5\\
x + 2y + z - 1 =  - x - 2y - z - 5
\end{array} \right.\\
 \Leftrightarrow 2x + 4y + 2z + 4 = 0
\end{array}\)

Tập hợp các điểm M là một mặt phẳng có phương trình : x + 2y + z + 2 = 0

---

Tìm khoảng cách giữa hai mặt phẳng Ax + By + Cz + D = 0 và Ax + By + Cz + D′ = 0 với D ≠ D′

Hướng dẫn giải:

Hai mặt phẳng đã cho song song với nhau.

Lấy M(x₀, y₀, z₀) thuộc mặt phẳng Ax + By + Cz + D = 0.

Ta có Ax₀ + By₀ + Cz₀ + D = 0 => Ax₀ + By₀ + Cz₀ = −D

Khoảng cách giữa hai mặt phẳng bằng khoảng cách từ điểm M đến mặt phẳng thứ hai, ta có:

\(d = \frac{{|A{x_0} + B{y_0} + C{z_0} + D\prime |}}{{\sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{|D\prime  - D|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\)

---

Tìm điểm M trên trục Oz trong mỗi trường hợp sau:

a) M cách đều điểm A(2 ; 3 ; 4) và mặt phẳng 2x + 3y + z − 17 = 0

b) M cách đều hai mặt phẳng x + y − z + 1 = 0 và x − y + z + 5 = 0

Hướng dẫn giải:

Câu a:

Giả sử M(0; 0; c) thuộc trục Oz

Ta có: \(MA = \sqrt {{2^2} + {3^2} + {{(4 - c)}^2}} \) và khoảng cách từ điểm M đến mặt phẳng đã cho là \(d = \frac{{|c - 17|}}{{\sqrt {{2^2} + {3^2} + {1^2}} }}\)

\(\begin{array}{l}
MA = d \Leftrightarrow \sqrt {13 + {{(4 - c)}^2}}  = \frac{{|c - 17|}}{{\sqrt {14} }}\\
 \Leftrightarrow 13 + {(4 - c)^2} = \frac{{{{(c - 17)}^2}}}{{14}} \Leftrightarrow c = 3.
\end{array}\)

Vậy M(0; 0; 3)

Câu b:

M(0; 0 ; c) cách đều hai mặt phẳng đã cho khi và chỉ khi:

\(\frac{{| - c + 1|}}{{\sqrt 3 }} = \frac{{|c + 5|}}{{\sqrt 3 }} \Leftrightarrow c =  - 2 \Rightarrow M(0;0; - 2)\)

---

Cho tứ diện OABC có các tam giác OAB, OBC, OCA là những tam giác vuông đỉnh O. Gọi α, β, γ  lần lượt là góc giữa mặt phẳng (ABC) và các mặt phẳng (OBC), (OCA), (OAB). Bằng phương pháp toạ độ, hãy chứng minh :

a) Tam giác ABC có ba góc nhọn.

b) \(co{s^2}\alpha  + co{s^2}\beta  + co{s^2}\gamma  = 1\)

Hướng dẫn giải:

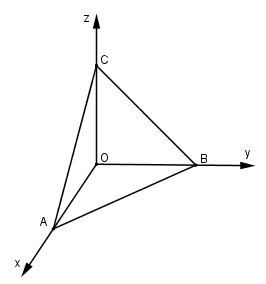
Câu a:

Chọn hệ trục tọa độ Oxyz như hình vẽ.

Ta có A(a; 0; 0), B(0; b; 0), C(0; 0; c) (a > 0, b > 0, c > 0) (a > 0, b > 0, c > 0)

Ta có 

\(\begin{array}{l}
\overrightarrow {AB}  = ( - a;b;0);\overrightarrow {AC}  = ( - a;0;c) \Rightarrow \overrightarrow {AB} .\overrightarrow {AC}  = {a^2} > 0\\
 \Rightarrow cosA = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{AB.AC}} > 0
\end{array}\)

=> A là góc nhọn

Tương tự các góc B, C của tam giác ABC cũng nhọn.

Câu b:

Mp(ABC) có phương trình \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) nên có vecto pháp tuyến \(\vec n = \left( {\frac{1}{a};\frac{1}{b};\frac{1}{c}} \right)\)

Mp(OBC) ≡ Mp(Oyz) có vectơ pháp tuyến \(\vec i = \left( {1;0;0} \right)\)

Gọi α là góc giữa mp(ABC) và mp(OBC) thì:

\({\cos ^2}\alpha  = {\left( {\frac{{\overrightarrow n .\overrightarrow i }}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow i } \right|}}} \right)^2} = \frac{{\frac{1}{{{a^2}}}}}{{\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}}}\)

Tương tự 

\({\cos ^2}\beta  = \frac{{\frac{1}{{{b^2}}}}}{{\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}}};{\cos ^2}\gamma  = \frac{{\frac{1}{{{c^2}}}}}{{\frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}}}\)

Vậy \(co{s^2}\alpha  + co{s^2}\beta  + co{s^2}\gamma  = 1\)

---

Viết phương trình mặt phẳng song song với mặt phẳng 4x + 3y − 12z + 1 = 0 và tiếp xúc với mặt cầu có phương trình: x² + y² + z² − 2x − 4y − 6z − 2 = 0

Hướng dẫn giải:

Ta có: 

\(\begin{array}{l}
{x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 2 = 0\\
 \Leftrightarrow {(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2} = 16
\end{array}\)

Mặt cầu có tâm I(1; 2; 3) bán kính R = 4.
Mặt phẳng (P) song song với mặt phẳng đã cho nên có phương trình 4x + 3y − 12z + D = 0 với D ≠ 1.
Mp(P) tiếp xúc với mặt cầu khi và chỉ khi khoảng cách d từ điểm I đến mp(P) bằng bán kính R.

\(\begin{array}{l}
d = \frac{{|4 + 6 - 36 + D|}}{{\sqrt {16 + 9 + 144} }} = 4 \Leftrightarrow \frac{{| - 26 + D|}}{{13}} = 4 \Leftrightarrow \\
 \Leftrightarrow \left[ \begin{array}{l}
 - 26 + D = 12\\
 - 26 + D =  - 12
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
D = 78\\
D =  - 26
\end{array} \right.
\end{array}\)

Vậy có 2 mặt phẳng thỏa yêu cầu bài toán:

4x + 3y - 12z + 78 = 0; 4x + 3y - 12z - 26 = 0

 

Trên đây là nội dung hướng dẫn giải chi tiết bài tập SGK nâng cao môn Toán 12 Chương 3 Bài 2 Phương trình mặt phẳng được trình bày rõ ràng, cụ thể với phương pháp ngắn gọn và khoa học. Hy vọng rằng đây sẽ là tài liệu hữu ích giúp các em học sinh lớp 12 học tập thật tốt!