Đề thi và đáp án tham khảo môn Toán tốt nghiệp THPT 2024 - Mã đề 107

1. ĐỀ THI

BỘ GIÁO DỤC VÀ ĐÀO TẠO Đề chính thức

KỲ THI TỐT NGHIỆP THPT NĂM 2024 Bài thi: TOÁN Thời gian làm bài: 90 phút (Không kể thời gian phát đề)

Mã đề thi: 107

Câu 1: Nghiệm của phương trình \({{2}^{2x}}={{2}^{x+6}}\) là

A. x = -6.

B. x = 2.

C. x = -2.

D x = 6.

Câu 2: Cho hình nón có bán kính đáy r = 3 và độ dài đường sinh l = 5. Chiều cao của hình nón đã

cho bằng

A \(\sqrt{34}\).

B. 4.

C. 2.

D. 5.

Câu 3: Nếu \(\int\limits_{-2}^{1}{f(x)dx=-1}\) và \(\int\limits_{1}^{7}{f(x)dx=-5}\) thì \(\int\limits_{-2}^{7}{f(x)dx}\) bằng

A. 4.

B.-4.

C. 5.

D. -6

Câu 4: Tập nghiệm của bất phương trình \({{\log }_{\frac{1}{2}}}\left( x+2 \right)>-1\) là

A. \(\left( 0;+\infty  \right)\)

B. \(\left( -\infty ;0 \right)\)

C. \(\left( -2;0 \right)\)

D. \(\left( -2;1 \right)\)

Câu 5: Cho khối chóp tứ giác có thể tích \(V=3{{a}^{3}}\) và diện tích đáy \(B={{a}^{2}}\). Chiều cao của khối chóp đã

cho bằng

A. 6a.

B. a.

C. 9a.

D 3a.

Câu 6: Cho hình trụ có diện tích xung quanh \({{S}_{xq}}=36\pi \) và chiều cao h = 6. Bán kính của hình trụ đã cho bằng

A.3.

B. 9.

C. 12

D. 6

Câu 7: Dãy số nào dưới đây là một cấp số cộng?

A. 1,3,5,7.

B. 1,2,3, - 4.

C. 1, 0, 2, 4.

D. 1, 3, 5, 10.

Câu 8: Cho hàm số y = f(x) có bảng biến thiên như sau:

Số điểm cực trị của hàm số đã cho là

A. 1.

B. 4.

C. 3.

D. 2.

Câu 9:  Trong không gian Oxyz, cho đường thẳng d: \(\frac{x+1}{1}=\frac{y-2}{-1}=\frac{z}{-3}\). Vectơ nào dưới đây là một vectơ chỉ phương của d?

A. \(\overrightarrow{{{u}_{1}}}=\left( 1;2;0 \right)\)

B. \(\overrightarrow{{{u}_{2}}}=\left( -1;2;0 \right)\)

C. \(\overrightarrow{{{u}_{3}}}=\left( 1;-1;-3 \right)\)

D. \(\overrightarrow{{{u}_{4}}}=\left( 1;1;3 \right)\)

Câu 10: Với a,b là các số thức dương tùy ý và  \(a\ne 1,{{\log }_{{{a}^{2}}}}{{b}^{2}}\) bằng

A. \({{\log }_{a}}{{b}^{4}}\)

B. \({{\log }_{{{a}^{4}}}}b\)

C. \({{\left( {{\log }_{a}}b \right)}^{2}}\)

D. \({{\log }_{a}}b\)

Câu 11: Cho số phức z có \(\overline{z}=-5+6t\). Phần ảo của z bằng

1. 6.
2. 5.
3. -6.
4. -5.

Câu 12: Có bao nhiêu cách sắp xếp 6 người thành một hàng ngang?

A. 1.

B. 720.

C. 6.

D. 36.

Câu 13: Trên khoảng \(\left( 0;+\infty  \right)\), đạo hàm của hàm số   là

A. \(y={{x}^{\frac{1}{7}}}\)

B. \(y'=\frac{1}{7}{{x}^{\frac{6}{7}}}\)

C. \(y'=\frac{7}{8}{{x}^{\frac{8}{7}}}\)

D. \(y'=\frac{1}{7}{{x}^{\frac{-6}{7}}}\)

Câu 14: Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong trong hình bên.

Số nghiệm thực của phương trình f(x) = z là

A. 0.

B. 2.

C. 4.

D. 3.

Câu 15: Trong không gian Oxyz, cho hai điểm A(1; – 2; 3) và B(3; 0; 1). Gọi (S) là mặt cầu nhận AB làm đường kính, tâm của (S) có tọa độ là

A. (2; -1; 2).

B. (-1; -1; 1).

C. (4; -2; 4).

D. (1; 1; -1).

Câu 16: Trên mặt phẳng tọa độ, M (2; - 5) là điểm biểu diễn của số phức z. Phần thực của z bằng

A. -5.

B. 5.

C. 2.

D. -2

Câu 17: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A. y = x³ + 3x² - 1.

B. y = x⁴ + 2x² -4.

C. \(y=\frac{x-2}{2x+1}.\)

D. y = -x³ + 3x² + 3.

Câu 18: Số phức z = i + i² + i³ bằng

A. 1.

B. -1.

C. -1 + 2i.

D. i.

Câu 19: Trong không gian Oxyz, mặt phẳng đi qua điểm M (3; 4; - 2) và vuông góc với trục Oz có phương trình là

A. x + y + z - 5=0.

B. z + 2 = 0.

C. x – 3 = 0.

D. y – 4 = 0.

Câu 20: Cho hàm số y = f(x) có đạo hàm f'(x) = 2x + 4, Vx ∈ \(\mathbb{R}\). Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Α. (2; 4).

B. \((-\infty ;-2)\).

C. \((2;+\infty )\).

D. \((-2;+\infty )\).

Câu 21: Hàm số nào dưới đây là hàm số mũ?

A. y = x²⁰²⁴

B. y = x^-4.

C. y = log₃x.

D. y = 2024^x.

Câu 22: Khẳng định nào dưới đây đúng?

A. \(\int{(2x+3)}\)dx = x² + 3x + C.

B. \(\int{(2x+3)}\)dx = \(\frac{1}{2}\)x² + 3x + C.

C. \(\int{(2x+3)}\)dx = 2x² + 3x + C.

D. \(\int{(2x+3)}\)dx = x² + C.

Câu 23: Trong không gian Oxyz, cho hai vecto \(\overrightarrow{a}\) = (2;3;-1) và \(\overrightarrow{b}\) = (-3; 2; -4). Vecto \(\overrightarrow{a}\) + \(\overrightarrow{b}\) có tọa độ là

A. (-1; -5; 5).

B. (1; -5; 5).

C. (-5; -1; -3).

D. (-1; 5; -5).

Câu 24: Cho hàm số y = f(x) có bảng biến thiên như sau:

Điểm cực tiểu của hàm số đã cho là

A. x = 2.

B. x = 1.

C. x = -1.

D. x = -2.

Câu 25: Tiệm cận đứng của đồ thị hàm số \(y=\frac{4x-1}{3x\text{ }+\text{ }2}\) có phương trình là

A. \(x=-\frac{2}{3}\)

B. \(y=-\frac{2}{3}.\)

C. \(x=\frac{4}{3}.\)

D. \(y=\frac{4}{3}.\)

Câu 26: Trên khoáng (-∞; + ∞), hàm số F(x) = \(\frac{1}{2}\) sin2x là một nguyên hàm của hàm số nào dưới đây?

A. f₂(x) = cos2x.

B. f₁(x) = - cos2x.

C. f₄(x) = -\(\frac{1}{4}\)cos2x.

D. f₃(x) = -\(\frac{1}{2}\)cos2x.

Câu 27: Cho hàm số f(x) có đạo hàm liên tục trên \(\mathbb{R}\) và f(1) = 3, f(2) = 1. Giá trị của \(\int\limits_{1}^{2}{f'(x)dx}\) bằng

A. -2.

B. 2.

C. -4.

D. 4.

Câu 28: Cho khối lăng trụ tạm giác có diện tích đáy B = 6 và chiều cao h = 3. Thể tích của khối lăng trụ đã cho bằng

A. 6.

B. 12.

C. 24.

D. 18.

Câu 29: Cho số phức z = 3 + 4i. Mô đun của số phức iz bằng

A. 49.

B. 7.

C. 5.

D. 25.

Câu 30: Cho hình chóp S .ABC có đáy là tam giác vuông cân tại A, BC = 2a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = \(\sqrt{3}a\). Góc giữa hai mặt phẳng (SBC) và (ABC) bằng

A. 30°.

B. 60°.

C. 90°.

D. 45°.

Câu 31: Giá trị lớn nhất của hàm số f(x) = - 6x³ + 27x² - 16x + 1 trên đoạn [1; 5) bằng

A. 6.

B. \(\frac{329}{9}\)

C. -154.

D. -\(\frac{14}{9}\).

Câu 32: Với a, b là hai số thực lớn hơn 1, log_ab b bằng

A. \(\frac{1}{1+{{\log }_{b}}a}.\)

B. 1 + log_ba.

C. \(\frac{1}{{{\log }_{b}}a}.\)

D. 1 – log_ba.

Câu 33: Một ô tô đang chuyển động với vận tốc 20 m/s thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động thẳng, chậm dần đều với vận tốc biến thiên theo thời gian được xác định bởi quy luật v(t) = - 4t + 20 (m/s) trong đó t là khoảng thời gian tính bằng giây kể từ lúc người lái xe bắt đầu đạp phanh. Quãng đường ô tô đi được từ lúc người lái xe bắt đầu đạp phanh đến khi xe dừng hẳn bằng

A. 32 m.

B. 48 m.

C. 30 m.

D. 50 m.

Câu 34: Cho hình chóp S. ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = \(\sqrt{2}a\). Khoảng cách từ C đến mặt phẳng (SBD) bằng

A. \(\frac{\sqrt{6}}{3}a.\)

B. \(\frac{\sqrt{10}}{5}a.\)

C. \(\frac{\sqrt{10}}{10}a.\)

D. \(\frac{2\sqrt{10}}{5}a.\)

Câu 35: Trên hai tia Ox, Oy của góc nhọn xOy lần lượt cho 5 điểm và 6 điểm phân biệt khác O. Chọn ngẫu nhiên 3 điểm từ 12 điểm (gồm điểm O và 11 điểm đã cho), xác suất để 3 điểm chọn được là ba đỉnh của một tam giác bằng

A. \(\frac{27}{44}.\)

B. \(\frac{3}{4}.\)

C. \(\frac{19}{22}.\)

D. \(\frac{39}{44}.\)

Câu 36: Trong không gian Oxyz, cho hai điểm A (1; 2; 3) và B (3; 2; 5). Gọi M là điểm thỏa mãn \(\overrightarrow{MB}=3\overrightarrow{MA}\), độ dài của vectơ \(\overrightarrow{OM}\)bằng

A. \(\frac{\sqrt{74}}{2}\)

B. \(2\sqrt{2}\)

C. 8

D. \(2\sqrt{14}\)

Câu 37: Cho hàm số bậc bốn y = f(x). Hàm số y = f'(x) có đồ thị là đường cong trong hình bên. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

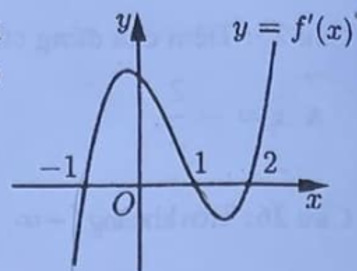
A. (–1;1)

B. (–1;2)

C. (1;2)

D. (–¥;–1)

Câu 38: Trong không gian Oxyz, cho điểm A (1; 2; - 1) và mặt phẳng (P): 2x – z + 1 = 0. Đường thẳng đi qua A và vuông góc với (P) có phương trình là:

A. \(\left\{ \begin{align} & x=2+t \\ & y=2t \\ & z=-1-t \\ \end{align} \right.\)

B. \(\left\{ \begin{align} & x=1+2t \\ & y=2 \\ & z=-1-t \\ \end{align} \right.\)

C. \( \left\{ \begin{align} & x=-1+2t \\ & y=-2 \\ & z=1-t \\ \end{align} \right.\)

D. \(\left\{ \begin{align} & x=1+2t \\ & y=2-t \\ & z=-1+t \\ \end{align} \right.\)

Câu 39: Cho hàm số y = f(x) có \(f\left( e \right)=\frac{1}{5}\) và \(f'\left( x \right)=\frac{1}{3}\ln x,\forall x\in \left( 0;+\infty  \right)\). Biết \(\int\limits_{e}^{{{e}^{3}}}{\frac{f\left( x \right)}{{{x}^{2}}}dx=a{{e}^{-3}}+b{{e}^{-1}}+c}\), với a, b, c là các số hữu tỉ, giá trị của a - b + c thuộc khoảng nào dưới đây?

A. \(\left( 0;\frac{1}{4} \right)\)

B. \(\left( \frac{1}{2};\frac{3}{4} \right)\)

C. \(\left( \frac{1}{4};\frac{1}{2} \right)\)

D. \(\left( \frac{3}{4};1 \right)\)

Câu 40: Có bao nhiêu nguyên tố a lớn hớn 1 sao cho ứng với mỗi a tồn tại không quá 4 số nguyên tố b thỏa mãn \({{5}^{{{b}^{2}}}}<{{25}^{-b}}.{{a}^{b+2}}\)

A. 99.

B. 100.

C. 125.

D. 124.

Câu 41: Cho hàm số bậc bốn y = f(x) có ba điểm cực trị là \(-\frac{3}{2};2;\frac{11}{2}\) và đạt giá trị nhỏ nhất trên \(\mathbb{R}\). Bất phương trình \(f\left( x \right)\le m\) có nghiệm thuộc đoạn [0; 3] khi và chỉ khi

A. \(m\ge f\left( 2 \right).\)

B. \(m\ge f\left( 0 \right).\)

C. \(f\left( 2 \right)\ge m\ge f\left( 3 \right).\)

D. \(m\ge f\left( 3 \right).\)

Câu 42: Trong không gian Oxyz, cho hai đường thẳng \({{d}_{1}}:\frac{x-2}{1}=\frac{y-4}{3}=\frac{z+3}{-5}\) và \({{d}_{2}}:\frac{x+2}{1}=\frac{y+2}{-1}=\frac{z+1}{-1}\). Trong các mặt cầu tiếp xúc với cả hai đường thẳng d₁ và d₂ gọi (S) là mặt cầu có bán kính nhỏ nhất, phương trình của (S) là

A. x² + (y + 1)² + z² = 6.

B. (x – 1)² + (y + 2)² + (z + 1)² = 6.

C. x² + (y – 3)² + (z + 4)² = 6.

D. (x + 1)² + y² + (z – 1)² = 6.

Câu 43: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, AB = 2a mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Diện tích của mặt cầu ngoại tiếp hình chóp đã cho bằng

A. \(\frac{28\pi }{3}{{a}^{2}}\)

B. \(\frac{28\pi }{9}{{a}^{2}}\)

C. \(\frac{25\pi }{3}{{a}^{2}}\)

D. \(\frac{25\pi }{9}{{a}^{2}}\)

Câu 44: Có bao nhiêu giá trị nguyên của tham số m sao cho ứng với mỗi m tồn tại đúng hai số phức z thỏa mãn \(\left| z-1-5i \right|+\left| z-1+5i \right|=10\) và \(\left| z-2-i \right|=m\)

A. 5.

B. 2.

C.3.

D. 4.

Câu 45: Xét hàm số \(f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d(a,b,c,d\in \mathbb{R},a>0)\) có hai điểm cực trị x₁ và x₂ (với x₁ < x₂ thỏa mãn x₁ + x₂ = 0. Hình phẳng giới hạn bởi đường y = f'(x)f''(x) và trục hoành có diện tích bằng \(\frac{9}{4}\)Biết \(\int\limits_{{{x}_{1}}}^{{{x}_{2}}}{\frac{f'\left( x \right)}{{{3}^{x}}+1}dx=-\frac{7}{2}}\), giá trị của \(\int\limits_{0}^{{{x}_{2}}}{\left( x+2 \right)f''\left( x \right)}dx\) thuộc khoảng nào dưới đây?

A. \(\left( -7;-6 \right)\)

B. \(\left( -1;0 \right)\)

C. \(\left( 0;1 \right)\)

D. \(\left( 6;7 \right)\)

Câu 46: Cho khối lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB = a. Biết góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 30⁰, thể tích của khối lăng trụ đã cho bằng

A. \(\frac{\sqrt{6}}{12}{{a}^{3}}\)

B. \(\frac{\sqrt{6}}{36}{{a}^{3}}\)

C. \(\frac{3\sqrt{6}}{4}{{a}^{3}}\)

D. \(\frac{\sqrt{6}}{4}{{a}^{3}}\)

Câu 47: Cho hàm số \(f\left( x \right)=\frac{2}{{{x}^{3}}}+\ln \frac{x+3}{x-3}\) bao nhiêu số nguyên \(a\in \left( -\infty ;2100 \right)\) thỏa mãn

\(f\left( a-2024 \right)+f\left( 6a-27 \right)\ge 0\)?

A. 2096.

B. 288.

C. 360.

D. 1807.

Câu 48: Xét phương trình bậc hai az² + bx + c = 0 (a, b, c ∈ R, a ≠ 0) có hai nghiệm phức z₁, z₂ có phần ảo khác 0 và \(\left| 2{{z}_{1}}-\frac{1}{9} \right|=\left| {{z}_{1}}-{{z}_{2}} \right|\). Giả sử \(\left| {{z}_{1}} \right|=\frac{1}{\sqrt{k}}\) và w là số phức thỏa mãn cw² + bw + a = 0, có bao nhiêu số nguyên dương k sao cho ứng với mỗi k tồn tại đúng 9 số phức z₃ có phần ảo nguyên, z₃ - w là số thuần ảo và \(\left| {{z}_{3}} \right|\le \left| w \right|\)?

A. 11

B. 12

C. 23

D. 22

Câu 49: Trong không gian Oxyz, cho hai điểm A(1;6; -1), B(2;-4;-1) và mặt cầu (S) tâm I(1;2;-1) đi qua A. Điểm M(a; b; c) (với c > 0) thuộc (S) sao cho IAM là tam giác tù, có diện tích bằng \(2\sqrt{7}\)và khoảng cách giữa hai đường thẳng BM và IA lớn nhất. Giá trị của a + b + c thuộc khoảng nào dưới đây?

A. \(\left( 2;\frac{5}{2} \right)\)

B. \(\left( \frac{3}{2};2 \right)\)

C. \(\left( 1;\frac{3}{2} \right)\)

D. \(\left( \frac{5}{2};3 \right)\)

Câu 50: Xét hàm số bậc bốn y = f(x) có f(-1) = -5. Hàm số y = f'(x) đồng biến trên khoảng \(\left( -\infty ;+\infty  \right)\), f'(4) = 0 và f'(-1) = a. Có bao nhiêu số nguyên \(a\in \left( -100;0 \right)\) sao cho ứng với mỗi a, hàm số \(\left| f\left( x \right)+\frac{5}{{{x}^{2}}} \right|\)có đúng 3 điểm cực trị thuộc khoảng \(\left( -100;0 \right)\)?

A. 90

B. 10

C. 9

D. 89

-----HẾT-----

 

1. D	2. B	3. D	4. C	5. C	6. A	7. A	8. C	9. C	10. D
11. C	12. B	13. D	14. C	15. A	16. C	17. A	18. B	19. B	20. B
21. D	22. A	23. D	24. C	25. A	26. A	27. A	28. D	29. C	30. B
31. B	32. A	33. D	34. B	35. B	36. B	37. A	38. B	39. C	40. D
41. B	42. D	43. A	44. C	45. D	46. A	47. B	48. D	49. A	50. B

 

Trên đây là toàn bộ nội dung Đề và đáp án đề thi tốt nghiệp THPT môn Toán năm 2024 - Mã đề 107. Để xem thêm nhiều tài liệu tham khảo hữu ích khác các em chọn chức năng xem online hoặc đăng nhập vào trang Hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Các em quan tâm có thể tham khảo thêm các tài liệu cùng chuyên mục:

• Đáp án tham khảo đề thi tốt nghiệp THPT môn Ngữ văn năm 2024
• Đề thi và đáp án tham khảo môn Tiếng Anh tốt nghiệp THPT 2024 - Mã đề 408

Chúc các em học tập tốt!