Bài tập 45 trang 163 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

Lời giải chi tiết

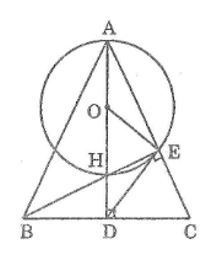
\(a)\) Gọi \(O\) là trung điểm của \(AH\)

Tam giác \(AEH\) vuông tại \(E\) có \(EO\) là đường trung tuyến nên:

\( EO = OA = OH =\displaystyle{{AH} \over 2}\) (tính chất tam giác vuông)

Vậy điểm \(E\) nằm trên đường tròn \(\left( \displaystyle{O;{{AH} \over 2}} \right)\)

\(b)\) Ta có: \(OH = OE\)

suy ra tam giác \(OHE\) cân tại \(O\)

suy ra: \(\widehat {OEH} = \widehat {OHE}\)       \( (1)\)

Mà \(\widehat {BHD} = \widehat {OHE}\) (đối đỉnh)  \((2)\)

Trong tam giác \(BDH\) ta có:

\(\widehat {HDB} = 90^\circ \)

Suy ra: \(\widehat {HBD} + \widehat {BHD} = 90^\circ \) \((3)\)

Từ \((1),\) \((2)\) và \((3)\) suy ra:

\(\widehat {OEH} + \widehat {HBD} = 90^\circ \)   \((4)\)

Tam giác \(ABC\) cân tại \(A\) có \(AD ⊥ BC\) nên AD là đường trung tuyến, suy ra \(BD = CD\)

Tam giác \(BCE\) vuông tại \(E\) có \(ED\) là đường trung tuyến nên:

\(ED = BD = \displaystyle{{BC} \over 2}\) (tính chất tam giác vuông).

Suy ra tam giác \(BDE\) cân tại \(D\)

Suy ra: \(\widehat {DBE} = \widehat {DEB}\)     \((5)\)

Từ \((4)\) và \((5)\) suy ra: \(\widehat {OEH} + \widehat {DEB} = 90^\circ \) hay \(\widehat {DEO} = 90^\circ \)

Suy ra: \(DE ⊥ EO.\) Vậy \(DE\) là tiếp tuyến của đường tròn \((O).\)

-- Mod Toán 9 HỌC247