Bài tập 5.2 trang 164 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

Lời giải chi tiết

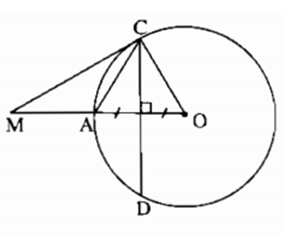
Vì dây \(CD\) vuông góc với  \(OA\) tại trung điểm của \(OA\) nên \(CD\) là đường trung trực của \(OA\)

Suy ra \(CA = CO.\)

Mà \(OA=OC\) (cùng bằng bán kính của đường tròn (O))

Và \(AO=MA\) ( vì \(M\) là điểm đối xứng với \(O\) qua \(A\))

Suy ra \(CA = CO = AO = AM=\dfrac{OM}2\)

Xét tam giác MCO có \(CA\) là đường trung tuyến ứng với cạnh MO và \(CA = \dfrac{OM}2\) nên tam giác MCO vuông tại C.

Suy ra \(\widehat {MCO} = 90^\circ \) hay \(MC\bot OC\) tại C. 

Vậy \(MC\) là tiếp tuyến của đường tròn \((O).\)

-- Mod Toán 9 HỌC247