Giải bài 36 tr 126 sách GK Toán 9 Tập 2
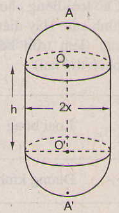
Một chi tiết máy gồm một hình trù và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị: cm)
a) Tìm một hệ thức giữa x và h khi AA' có độ dài không đổi và bằng 2a.
b) Với điều kiện ở a) hãy tính diện tích bề mặt và thể tích của chi tiết theo x và a.
Hướng dẫn giải chi tiết bài 36
Bài 36 yêu cầu chúng ta tính thể tích của bề mặt và chi tiết theo các độ dài đại số là các biến số.
Câu a:
Ta có hệ thức liên hệ giữa x và h là:
\(\small h + 2x = 2a\)
Câu b:
Diện tích cần tính gồm diện tích xung quanh của hình trụ có bán kính đáy là x, chiều cao là h và diện tích mặt cầu có bán kính là x.
Diện tích xung quanh của hình trụ:
\(\small S_t=2\pi.x.h\)
Diện tích mặt cầu:
\(\small S_c=4.\pi.x^2\)
Nên diện tích bề mặt của chi tiết máy là:
\(\small S=S_t+S_c=2\pi.x.h+4\pi.x^2=2\pi.x.(h+2x)=4\pi.a.x\)
Thể tích cần tình gồm thể tích hình trù và thể tích hình cầu. Ta có:
\(\small V_t=\pi.x^2.h\)
\(\small V_c=\frac{4}{3}\pi.x^3\)
Nên thể tích của chi tiết máy là:
\(\small V=V_t+V_c=\pi.x^2.h+\frac{4}{3}.\pi.x^3=2\pi.x^2.a-\frac{2}{3}\pi.x^3\)
-- Mod Toán 9 HỌC247
-


Cho hình lập phương ABCDA'B'C'D' có đường chéo bằng 2√3 a. Tính diện tích mặt cầu nội tiếp hình lập phương đó:
A. 8πa^2
B. 4πa^2/3
C. 4πa^2
D. 8√3 πa^2
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 34 trang 125 SGK Toán 9 Tập 2
Bài tập 35 trang 126 SGK Toán 9 Tập 2
Bài tập 37 trang 126 SGK Toán 9 Tập 2
Bài tập 27 trang 169 SBT Toán 9 Tập 2
Bài tập 28 trang 170 SBT Toán 9 Tập 2
Bài tập 29 trang 170 SBT Toán 9 Tập 2
Bài tập 30 trang 170 SBT Toán 9 Tập 2
Bài tập 31 trang 171 SBT Toán 9 Tập 2
Bài tập 32 trang 171 SBT Toán 9 Tập 2
Bài tập 33 trang 171 SBT Toán 9 Tập 2
Bài tập 34 trang 171 SBT Toán 9 Tập 2
Bài tập 35 trang 172 SBT Toán 9 Tập 2
Bài tập 36 trang 172 SBT Toán 9 Tập 2
Bài tập 37 trang 173 SBT Toán 9 Tập 2
Bài tập 38 trang 173 SBT Toán 9 Tập 2
Bài tập 39 trang 173 SBT Toán 9 Tập 2






