Hướng dẫn Giải bài tập Toán 7 Chân trời sáng tạo Chương 8 Bài 8 Tính chất ba đường cao của tam giác giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động khám phá 1 trang 77 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Em hãy dựng tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B đến cạnh AC của tam giác.
-
Thực hành 1 trang 77 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC
-
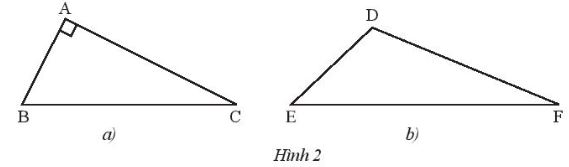
Vận dụng 1 trang 77 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a)
Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b)
-
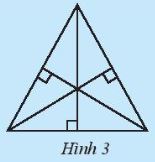
Hoạt động khám phá 2 trang 77 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.
-
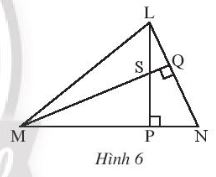
Thực hành 2 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc với ML.
-
Vận dụng 2 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có ba đường cao AD, BE, CF đồng qui tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
-
Giải bài 1 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.
-
Giải bài 2 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
-
Giải bài 3 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:
a) DE vuông góc với BC
b) BE vuông góc với DC
-
Giải bài 4 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
-
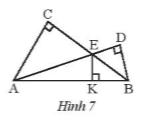
Giải bài 1 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Trong hình 7. Hãy chứng minh AC, EK và BD cùng đi qua một điểm.
-
Giải bài 2 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC cân tại A, vẽ đường trung tuyến AM. Qua A vẽ đường thẳng d vuông góc với AM. Chứng minh d // BC.
-
Giải bài 3 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Vẽ hai đường cao AE và AF của hai tam giác Abc và ACD. Chứng minh góc EAF vuông.
-
Giải bài 4 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác ABC có \(\widehat {{A^{}}} = {65^o},\widehat B = {54^o}\). Vẽ trực tâm H của tam giác ABC, Tính góc AHB.
-
Giải bài 5 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Cho tam giác Abc cân tại A có góc A nhọn và H là trực tâm. Cho biết \(\widehat {BHC} = {150^o}\). Tính các góc của tam giác ABC.