Giải bài 2 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2
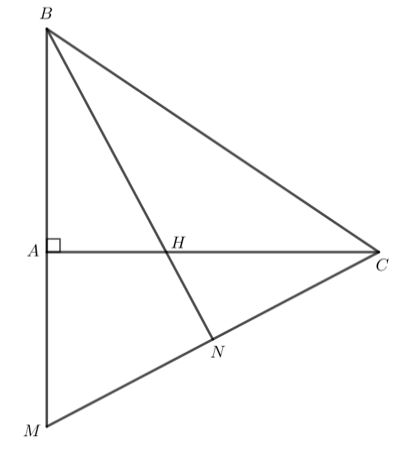
Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
- Ta chứng minh H là trực tâm của tam giác AMC
- Từ đó ta chứng minh MH vuông góc với BC
Lời giải chi tiết
Tam giác BMC có BM = BC nên tam giác BMC cân tại B.
Tam giác BMC cân tại B, có BN là đường phân giác nên BN cũng là đường cao của tam giác BMC.
Do đó BNMC.
Tam giác BMC có CABM, BNMC nên CA, BN là hai đường cao của tam giác BMC.
Mà CA và BN cắt nhau tại H nên H là trực tâm của tam giác BMC.
Do đó MHBC.
-- Mod Toán 7 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Vận dụng 2 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 63 SBT Toán 7 Chân trời sáng tạo tập 2 - CTST