Luyện tập 8 trang 23 SGK Toán 11 Tập 2 Cánh diều
Một hộp có 5 viên bi màu xanh, 6 viên bi màu đỏ và 7 viên bi màu vàng. Chọn ngẫu nhiên 5 viên bi trong hộp. Tính xác suất để 5 viên bi được chọn có đủ ba màu và số bi màu đỏ bằng số bi màu vàng?
Hướng dẫn giải chi tiết Luyện tập 8
- Mỗi cách chọn ra đồng thời 5 viên bi trong hộp có 5 + 6 + 7 = 18 viên bi cho ta một tập hợp chập 5 của 18 phần tử.
Do đó, không gian mẫu \(Ω\) gồm các tổ hợp chập 5 của 18 phần tử và = 8 458.
- Xét biến cố \(A\): “Chọn được 5 viên bi có đủ ba màu và số bi màu đỏ bằng số bi màu vàng”.
Sơ đồ hình cây biểu thị các khả năng thuận lợi cho biến cố \(A\):
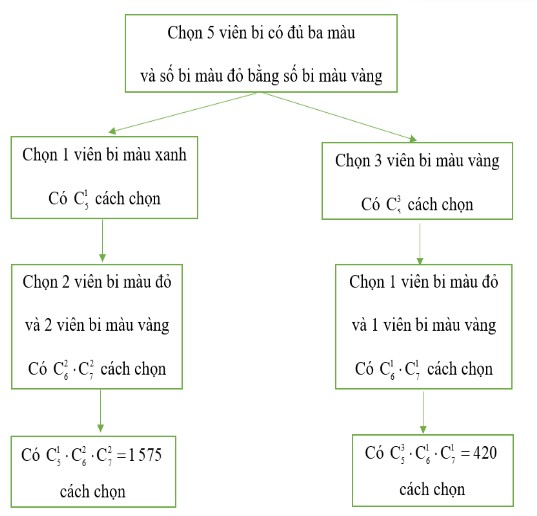
Như vậy, số kết quả thuận lợi cho biến cố \(A\) là: \(n(A) = 1 575 + 420 = 1 995\).
Vậy xác suất của biến cố \(A\) là: \(P(A)\) = .
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Luyện tập 7 trang 22 SGK Toán 11 Tập 2 Cánh diều - CD
Hoạt động 7 trang 22 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 1 trang 24 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 2 trang 24 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 3 trang 24 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 4 trang 24 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 5 trang 24 SGK Toán 11 Tập 2 Cánh diều - CD
Bài 6 trang 24 SGK Toán 11 Tập 2 Cánh diều - CD
Bài tập 6 trang 16 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 7 trang 17 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 8 trang 17 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 9 trang 18 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 10 trang 18 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 11 trang 18 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 12 trang 18 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 13 trang 18 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 14 trang 18 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 15 trang 18 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 16 trang 19 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 17 trang 19 SBT Toán 11 Tập 2 Cánh diều - CD
Bài tập 18 trang 19 SBT Toán 11 Tập 2 Cánh diều - CD





