Phần hướng dẫn giải bài tập Toán 11 Cánh Diều Chương 1 Hàm số lượng giác và Phương trình lượng giác sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Toán 11 Cánh Diều.
-
Giải Bài 1 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Hàm số y = sinx đồng biến trên khoảng:
A. \(\left( {0;\pi } \right)\)
B. \(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\)
C. \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
D. \(\left( { - \pi ;0} \right)\)
-
Giải Bài 2 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Hàm số nghịch biến trên khoảng \(\left( {\pi ;2\pi } \right)\) là:
A.\(y = \sin x\)
B.\(y = \cos x\)
C.\(y = \tan x\)
D.\(y = \cot x\)
-
Giải Bài 3 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Nếu \(\tan \left( {a + b} \right) = 3,\tan \left( {a - b} \right) = - 3\) thì \(\tan 2a\) bằng:
A.0
B.\(\frac{3}{5}\)
C.1
D.\( - \frac{3}{4}\)
-
Giải Bài 4 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Nếu \(\cos a = \frac{1}{4}\) thì \(\cos 2a\) bằng:
A.\(\frac{7}{8}\)
B.\( - \frac{7}{8}\)
C.\(\frac{{15}}{{16}}\)
D.\( - \frac{{15}}{{16}}\)
-
Giải Bài 5 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Nếu \(\cos a = \frac{3}{5}\) và \(\cos b = - \frac{4}{5}\) thì \(\cos \left( {a + b} \right)\cos \left( {a - b} \right)\) bằng:
A.0
B.2
C.4
D.5
-
Giải Bài 6 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Nếu \(\sin a = - \frac{{\sqrt 2 }}{3}\) thì \(\sin \left( {a + \frac{\pi }{4}} \right) + \sin \left( {a - \frac{\pi }{4}} \right)\) bằng
A.\(\frac{2}{3}\)
B.\(\frac{1}{3}\)
C.\( - \frac{2}{3}\)
D.\( - \frac{1}{3}\)
-
Giải Bài 7 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Số nghiệm của phương trình cosx = 0 trên đoạn \(\left[ {0;10\pi } \right]\) là
A.5
B.9
C.10
D.11
-
Giải Bài 8 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Số nghiệm của phương trình sinx = 0 trên đoạn \(\left[ {0;10\pi } \right]\) là:
A.10
B.6
C.5
D.11
-
Giải Bài 9 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Phương trình \(\cot x = - 1\) có nghiệm là:
A.\( - \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
B.\(\frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
C.\(\frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
D.\( - \frac{\pi }{4} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
-
Giải Bài 10 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Số nghiệm của phương trình \(\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) trên đoạn \(\left[ {0;\pi } \right]\) là:
A.4
B.1
C.2
D.3
-
Giải Bài 11 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Vẽ đồ thị hàm số \(y = \cos x\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) rồi xác định số nghiệm của phương trình 3cosx + 2 = 0 trên đoạn đó.
-
Giải Bài 12 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Giải các phương trình sau:
a) \(\sin \left( {2x - \frac{\pi }{6}} \right) = - \frac{{\sqrt 3 }}{2}\)
b) \(\cos \left( {\frac{{3x}}{2} + \frac{\pi }{4}} \right) = \frac{1}{2}\)
c) \(\sin 3x - \cos 5x = 0\)
d) \({\cos ^2}x = \frac{1}{4}\)
e) \(\sin x - \sqrt 3 \cos x = 0\)
f) \(\sin x + \cos x = 0\)
-
Giải Bài 13 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày \(\left( {0 \le t < 24} \right)\) cho bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\). Tìm t để độ sâu của mực nước là
a) 15m
b) 9m
c) 10,5m
-
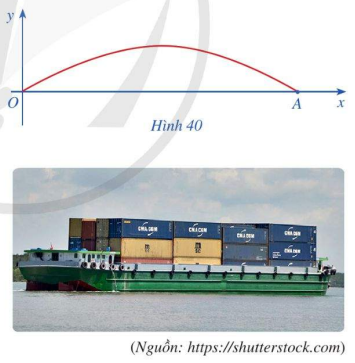
Giải Bài 14 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
a) Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Tìm chiều rộng đó (Làm tròn kết quả đến hàng phần mười)
b) Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 3,6m so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều rộng của khối hàng hóa đó phải nhỏ hơn 13,1m.
c) Một sà lan khác cũng chở khối hàng hóa được xếp thành hình hộp chữ nhật với chiều rộng của khối hàng hóa đó là 9m sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều cao của khối hàng hóa đó phải nhỏ hơn 4,3m
-
Bài tập 63 trang 31 SBT Toán 11 Tập 1 Cánh diều - CD
Cho lục giác đều \(ABCDEF\) nội tiếp trong đường tròn lượng giác (thứ tự đi từ \(A\) đến các đỉnh theo chiều dương). Khi đó, số đo của góc lượng giác \(\left( {OA,OC} \right)\) bằng:
A. \(\frac{{2\pi }}{3} + k2\pi \)
B. \( - \frac{{2\pi }}{3} + k2\pi \)
C. \(\frac{\pi }{3} + k2\pi \)
D. \( - \frac{\pi }{3} + k2\pi \)
-
Bài tập 64 trang 31 SBT Toán 11 Tập 1 Cánh diều - CD
Cho \(\tan \alpha = 2\). Giá trị của biểu thức \(A = \frac{{3\sin \alpha + \cos \alpha }}{{\sin \alpha - \cos \alpha }}\) bằng bao nhiêu?
-
Bài tập 65 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Giá trị của biểu thức \(A = {\left( {2\sin x - \cos x} \right)^2} + {\left( {2\cos x + \sin x} \right)^2}\) bằng:
A. 5
B. 3
C. 4
-
Bài tập 66 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Nếu hai góc \(a\) và \(b\) có \(\tan a = \frac{1}{3}\) và \(\tan b = \frac{1}{2}\) thì giá trị của \(\tan \left( {a - b} \right)\) bằng:
A. \(\frac{1}{7}\)
B. \( - \frac{1}{5}\)
C. \( - \frac{1}{7}\)
-
Bài tập 67 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Nếu \(\cos 2\alpha = \frac{{\sqrt 3 }}{6}\) thì giá trị của biểu thức \(\cos \left( {\alpha + \frac{\pi }{3}} \right)\cos \left( {\alpha - \frac{\pi }{3}} \right)\) bằng:
A. \(\frac{{\sqrt 3 }}{3}\)
B. \(\frac{{ - 3 + \sqrt 3 }}{{12}}\)
C. \( - \frac{{\sqrt 3 }}{3}\)
D. \(\frac{{3 + \sqrt 3 }}{{12}}\)
-
Bài tập 68 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Phương trình \(\cos 2x = 0\) có các nghiệm là:
A. \(x = \frac{\pi }{2} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\)
B. \(x = \frac{\pi }{4} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\)
C. \(x = \frac{\pi }{4} + k\frac{\pi }{2}{\rm{ }}\left( {k \in \mathbb{Z}} \right)\)
D. \(x = k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\)
-
Bài tập 69 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Phương trình \(\tan x = - \frac{1}{{\sqrt 3 }}\) có các nghiệm là:
A. \(x = \frac{\pi }{6} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\)
B. \(x = - \frac{\pi }{6} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\)
C. \(x = \frac{\pi }{3} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\)
D. \(x = - \frac{\pi }{3}k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\)
-
Bài tập 70 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Chứng minh mỗi đẳng thức sau là đúng:
a) \(\sin {45^o}.\cos {30^o} + \cos \left( { - {{45}^o}} \right).\sin \left( { - {{30}^o}} \right) = \sin {15^o}\)
b) \(\tan \frac{{9\pi }}{{20}} = \frac{{1 + \tan \frac{\pi }{5}}}{{1 - \tan \frac{\pi }{5}}}\)
-
Bài tập 71 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Cho \(\sin \left( {{{45}^o} - \alpha } \right) = \frac{1}{{2\sqrt 2 }}\).
a) Chứng minh rằng \({\sin ^2}\left( {{{45}^o} - \alpha } \right) = \frac{{1 - \sin 2\alpha }}{2}\)?
b) Tính \(\sin 2\alpha \)?
-
Bài tập 72 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Giải phương trình:
a) \(\sin \left( {2x - \frac{\pi }{6}} \right) = - \frac{1}{2}\)
b) \(\sin \left( {\frac{x}{3} + \frac{\pi }{2}} \right) = \frac{{\sqrt 3 }}{2}\)
c) \(\cos \left( {2x + \frac{\pi }{5}} \right) = \frac{{\sqrt 2 }}{2}\)
d) \(2\cos \frac{x}{2} + \sqrt 3 = 0\)
e) \(\sqrt 3 \tan \left( {2x + \frac{\pi }{3}} \right) - 1 = 0\)
g) \(\cot \left( {3x + \pi } \right) = - 1\)
-
Bài tập 73 trang 33 SBT Toán 11 Tập 1 Cánh diều - CD
Giải phương trình:
a) \(\sin \left( {2x + \frac{\pi }{3}} \right) = \sin \left( {3x - \frac{\pi }{6}} \right)\)
b) \(\cos \left( {x + \frac{\pi }{4}} \right) = \cos \left( {\frac{\pi }{4} - 2x} \right)\)
c) \({\cos ^2}\left( {\frac{x}{2} + \frac{\pi }{6}} \right) = {\cos ^2}\left( {\frac{{3x}}{2} + \frac{\pi }{4}} \right)\)
d) \(\cot 3x = \tan \frac{{2\pi }}{7}\)
-
Bài tập 74 trang 33 SBT Toán 11 Tập 1 Cánh diều - CD
Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm. Khoảng cách \(h\) (cm) từ chất điểm đến trục hoành được tính theo công thức \(h = \left| y \right|\), trong đó \(y = a\sin \left( {\frac{\pi }{5}t} \right)\), với \(t\) là thời gian chuyển động của chất điểm tính bằng giây \(\left( {t \ge 0} \right)\) và chất điểm bắt đầu chuyển động từ vị trí \(A\) (Xem hình dưới)
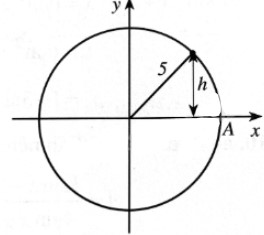
a) Chất điểm chuyển động một vòng hết bao nhiêu giây?
b) Tìm giá trị của \(a\).
c) Tìm thời điểm sao cho chất điểm ở vị trí có \(h = 2,5\) cm và nằm phía dưới trục hoành trong một vòng quay đầu tiên.






