Bài tập 63 trang 31 SBT Toán 11 Tập 1 Cánh diều
Cho lục giác đều \(ABCDEF\) nội tiếp trong đường tròn lượng giác (thứ tự đi từ \(A\) đến các đỉnh theo chiều dương). Khi đó, số đo của góc lượng giác \(\left( {OA,OC} \right)\) bằng:
A. \(\frac{{2\pi }}{3} + k2\pi \)
B. \( - \frac{{2\pi }}{3} + k2\pi \)
C. \(\frac{\pi }{3} + k2\pi \)
D. \( - \frac{\pi }{3} + k2\pi \)
Hướng dẫn giải chi tiết Bài tập 63
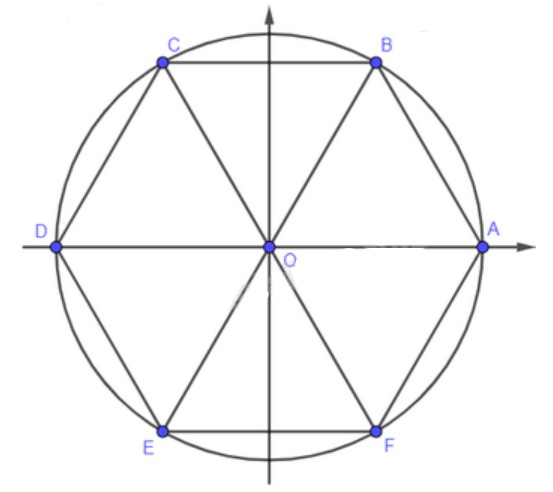
Vì lục giác đều \(ABCDEF\) nội tiếp đường tròn lượng giác tâm \(O\).
Nên ta có 6 góc bằng nhau: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = {60^o} = \frac{\pi }{3}\).
Do đó \(\widehat {AOC} = \frac{{2\pi }}{3} \Rightarrow \left( {OA,OC} \right) = \frac{{2\pi }}{3} + k2\pi \).
Đáp án đúng là A.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải Bài 13 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Giải Bài 14 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD
Bài tập 64 trang 31 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 65 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 66 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 67 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 68 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 69 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 70 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 71 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD
Bài tập 72 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD





