Bài tập 58 trang 178 SGK Toán 11 NC

Lý thuyết10 Trắc nghiệm

52 BT SGK

322 FAQ

Tìm giới hạn của dãy số (u_n) xác định bởi:

${u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{n\left( {n + 1} \right)}}$.

Hướng dẫn: Với mỗi số nguyên dương k, ta có

$\frac{1}{{k\left( {k + 1} \right)}} = \frac{1}{k} - \frac{1}{{k + 1}}$

Hướng dẫn giải chi tiết

$\begin{array}{l}
{u_n} = \left( {1 - \frac{1}{2}} \right) + \left( {\frac{1}{2} - \frac{1}{3}} \right) + ... + \\
\left( {\frac{1}{{n - 1}} - \frac{1}{n}} \right) + \left( {\frac{1}{n} - \frac{1}{{n + 1}}} \right) = 1 - \frac{1}{{n + 1}}
\end{array}$

Do đó $\lim {u_n} = \lim \left( {1 - \frac{1}{{n + 1}}} \right) = 1$

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 58 trang 178 SGK Toán 11 NC HAY thì click chia sẻ

YOMEDIA

Tìm a và b sao cho lim(căn bậc 3(an^3+(a-1)n^2+a-1)-căn(n^2+bn+2))=4

bởi Phu Ty 04/01/2020

Giải giúp mình 2 bài với

Theo dõi (1) 0 Trả lời
Tính lim(căn bậc 3(n^3-n^2)-căn(n^2+1))

bởi Phu Ty 04/01/2020

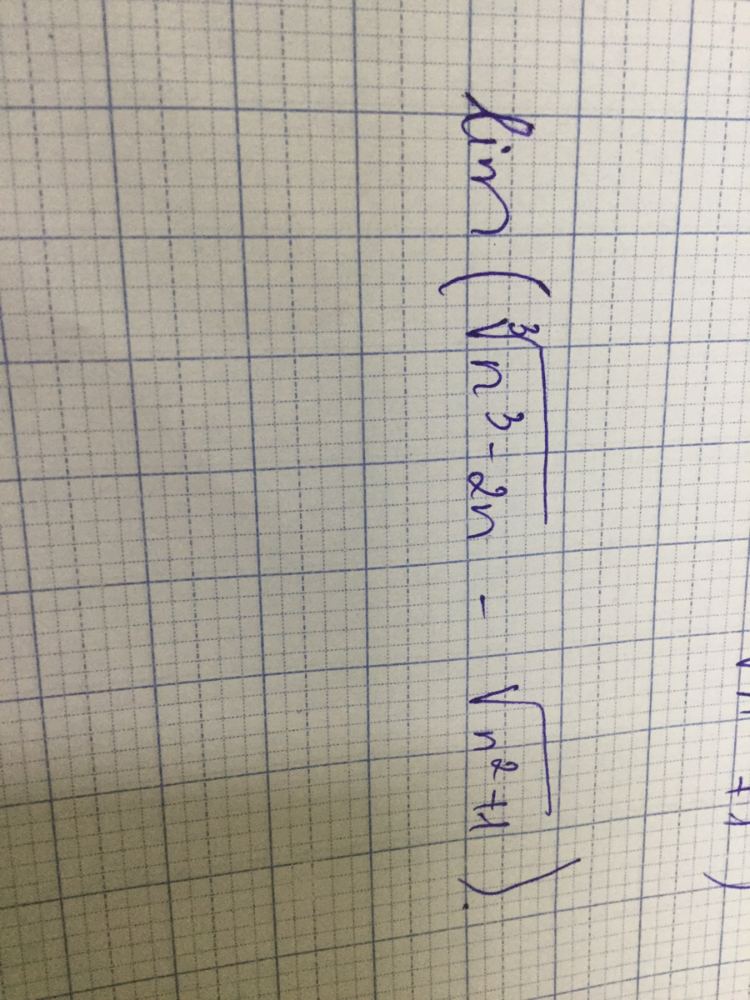Theo dõi (0) 0 Trả lời
Tìm giới hạn của căn f(x)-3/(x-2).(căn (f(x)-5)+3) khi x tiến tới 2

bởi Vũ Nhung 29/03/2019
Cho đa thức thoả mãn $\lim_{x->2}\frac{f(x)-9}{x-2}=15$ . Tìm $\lim_{x->2}\frac{\sqrt{f(x) }-3}{(x-2)(\sqrt{f(x)-5} +3)}=?$
1. A. 3
2. B. 1/2
3. C.15
4. D.0
Theo dõi (0) 3 Trả lời
Tính giới hạn H=((x^2+1)^2019+(x+1)^2019-2^2020)(x-1).(x+2018)

bởi Vũ Nhung 29/03/2019
Tính giới hạn H = $\lim_{x->1}\frac{(x^{2}+1)^{2019}+(x+1)^{2019}-2^{2020}}{(x-1)(x+2018)}$
1. A. $3.2^{2018}$
2. B. $2019.2^{2018}$
3. C. $3.2^{2019}$
4. D. $2^{2018}$
Theo dõi (0) 5 Trả lời
Tìm giới hạn của (x^4-1)/(x^3-2x^2+x)

bởi Mai Thuy 24/10/2018

$\lim\limits_{x\rightarrow1}$$\dfrac{x^4-1}{x^3-2x^2+x}$

Theo dõi (0) 1 Trả lời
Tìm giới hạn của (căn(2x^2-2)-căn(4x-3)+2x-7)/(9-x^2)

bởi Lan Anh 24/10/2018

1) lim(2x-1-$\sqrt{4x^2-4x-3}$)

2) lim$\dfrac{\sqrt{2x^2-2}-\sqrt{4x-3}+2x-7}{9-x^2}$

3) lim($x^3-1\sqrt{\dfrac{x}{x^2-1}}$

Giúp giùm mình đi mấy bạn

Theo dõi (0) 1 Trả lời
Tính giới hạn (căn 3.sinx-cosx)/sin(pi/3-2x)

bởi bich thu 26/10/2018

tính giới hạn sau:

$\lim\limits_{x\rightarrow\dfrac{\pi}{6}}\dfrac{\sqrt{3}sinx-cosx}{sin\left(\dfrac{\pi}{3}-2x\right)}$

Theo dõi (0) 1 Trả lời