Bài tập 56 trang 177 SGK Toán 11 NC
Tìm các giới hạn của các dãy số (un) với:
a) \({u_n} = \sqrt {3n - 1} - \sqrt {2n - 1} \)
b) \({u_n} = \frac{{{4^n} - {5^n}}}{{{2^n} + {{3.5}^n}}}\)
Hướng dẫn giải chi tiết
a)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\lim {u_n} = \lim \left( {\sqrt {3n - 1} - \sqrt {2n - 1} } \right)\\
= \lim \frac{{3n - 1 - \left( {2n - 1} \right)}}{{\sqrt {3n - 1} + \sqrt {2n - 1} }}
\end{array}\\
{ = \lim \frac{n}{{\sqrt n \left( {\sqrt {3 - \frac{1}{n}} + \sqrt {2 - \frac{1}{n}} } \right)}}}\\
{ = \lim \frac{{\sqrt n }}{{\sqrt {3 - \frac{1}{n}} + \sqrt {2 - \frac{1}{n}} }} = + \infty }
\end{array}\)
(vì \(\lim \sqrt n = + \infty ,lim\left( {\sqrt {3 - \frac{1}{n}} + \sqrt {2 - \frac{1}{n}} } \right) = \sqrt 3 + \sqrt 2 > 0\))
b)
\(\begin{array}{l}
\lim {u_n} = \lim \frac{{{4^n} - {5^n}}}{{{2^n} + {{3.5}^n}}}\\
= \lim \frac{{{{\left( {\frac{4}{5}} \right)}^n} - 1}}{{{{\left( {\frac{2}{5}} \right)}^n} + 3}} = - \frac{1}{3}
\end{array}\)
(vì \(\lim {\left( {\frac{4}{5}} \right)^n} = 0,\lim {\left( {\frac{2}{5}} \right)^n} = 0\))
-- Mod Toán 11 HỌC247
-


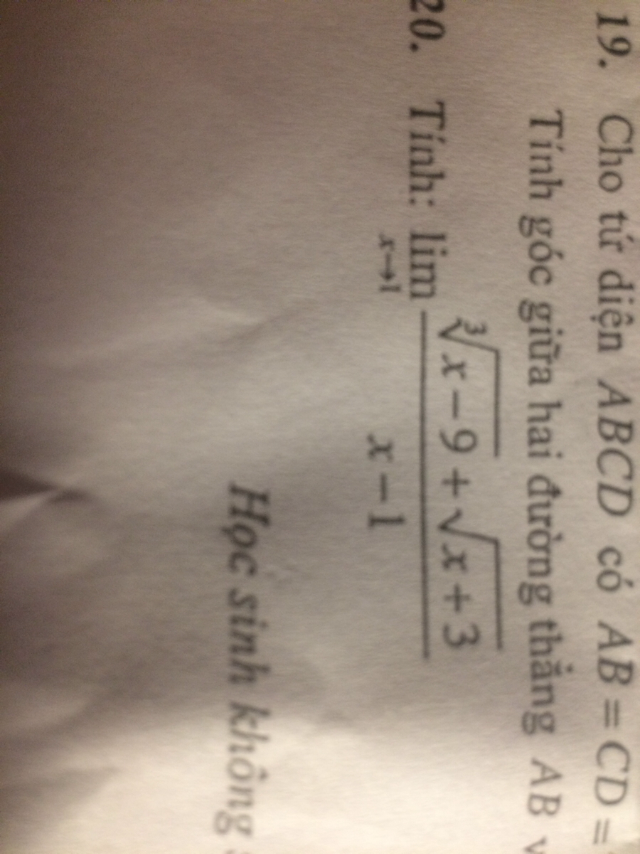 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


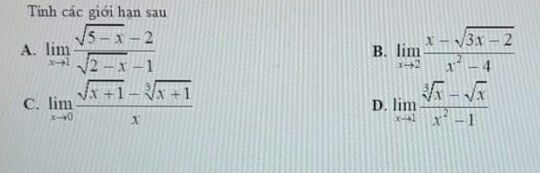
Tính giới hạn khi x->1 của căn(5-x)-2/căn(2-x)-1
bởi Linh Giang
 21/03/2020
21/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính giới hạn hàm số (1+2+3+4+...+n)/(1-3n^2).
bởi Hạ An Sơ
 20/03/2020
20/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Kiểm tra 1 tiết chương 4
bởi Ly Ly
 16/03/2020
16/03/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm giới hạn lim (4*3^n+7mũ (n+1))/(2.5mũ n+7 mũ n)
bởi Hạ An Sơ
 08/03/2020
08/03/2020
Mọi người giúp mình với!!!
 Theo dõi (1) 7 Trả lời
Theo dõi (1) 7 Trả lời -


Tìm giới hạn của: lim(2n-3)/(căn 3(n^3-2n)+1)
bởi Nhi Nguyễn
 28/02/2020
28/02/2020
Tìm giới hạn của: lim(2n-3)/(3√(n3-2n)+1)
Giải chi tiết giúp mình với.
Theo dõi (0) 3 Trả lời -


Tính lim n.căn(1+2+3+...+2n)/(3n^2+n-2)
bởi Anh Nhật
 26/02/2020
26/02/2020
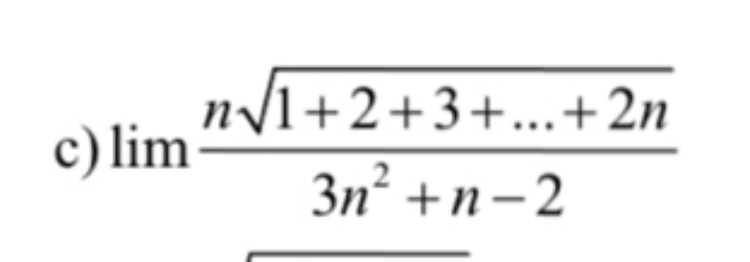 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 4.71 trang 176 SBT Toán 11
Bài tập 55 trang 177 SGK Toán 11 NC
Bài tập 57 trang 177 SGK Toán 11 NC
Bài tập 58 trang 178 SGK Toán 11 NC
Bài tập 59 trang 178 SGK Toán 11 NC
Bài tập 60 trang 178 SGK Toán 11 NC
Bài tập 61 trang 178 SGK Toán 11 NC
Bài tập 62 trang 178 SGK Toán 11 NC
Bài tập 63 trang 179 SGK Toán 11 NC
Bài tập 64 trang 179 SGK Toán 11 NC





