Giải bài 2 tr 29 sách GK Toán Hình lớp 11
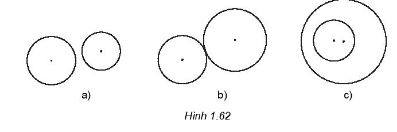
Tìm tâm vị tự của hai đường tròn trong các trường hợp sau:
Hướng dẫn giải chi tiết bài 2
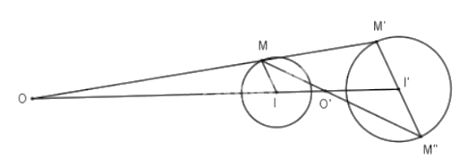
Lấy điểm M thuộc đường tròn (I). Qua I' kẻ đường thẳng song song với IM, đường thẳng này cắt đường tròn (I') tại M' và M''. Hai đường thẳng MM' và MM'' cắt đường thẳng II' theo thứ tự O và O'. Khi đó, O và O' là các tâm vị tự cần tìm
Vì hai đường tròn đã cho có bán kính khác nhau nên chúng có hai tâm vị tự là O và O', xác định trong từng trường hợp như sau ( xem hình vẽ):
Câu a:
Gọi hai đường trìn trên lần lượt là (I'; R') và (I; R). Trên (I; R) lấy điểm M, qua I' dựng đường thẳng song song với IM cắt (I'; R') tại M', M'' giả sử M và M' cùng phía đối với II', M, M'' khác phía đối với II'. Khi đó O và O1 lần lượt là giao điểm của MM', MM'' với II' là tâm vị tự của hai đường tròn.
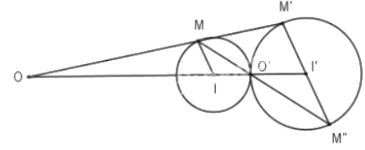
Câu b:
Làm tương tự câu a, ta có O vẫn là giao điểm nằm ngoài đoạn II' của MM' với II', tâm vị tự trong O1 chính là tiếp điểm của hai đường tròn.
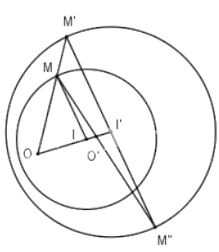
Câu c:
-- Mod Toán 11 HỌC247
-


Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(d\) có phương trình \(2x+y-4=0\). Hãy viết phương trình của đường thẳng \(d_1\) là ảnh của \(d\) qua phép vị tự tâm \(O\) tỉ số \(k=3\).
bởi Quynh Nhu
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = 2 biến đường tròn (C) có phương trình: \({x^2} + {y^2} + 4x + 6y = 12\) thành đường tròn (C’) có phương trình:
bởi Dell dell
 22/01/2021
22/01/2021
A. (x - 4)2 + (y - 6)2 = 100
B. (x + 2)2 + (y + 3)2 = 100
C. (x + 4)2 + (y + 6)2 = 100
D. (x - 2)2 + (y - 3)2 = 100
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -2, biến đường tròn (C) có phương trình: \({x^2} + {y^2} = 9\) thành đường tròn (C’) có phương trình:
bởi Nguyễn Thanh Trà
 22/01/2021
22/01/2021
A. x2 + y2 = 18
B. x2 + y2 = 36
C. x2 + y2 = 9
D. x2 + y2 = 6
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 29 SGK Hình học 11
Bài tập 3 trang 29 SGK Hình học 11
Bài tập 1.24 trang 33 SBT Hình học 11
Bài tập 1.25 trang 33 SBT Hình học 11
Bài tập 1.26 trang 33 SBT Hình học 11
Bài tập 1.23 trang 33 SBT Hình học 11
Bài tập 25 trang 29 SGK Hình học 11 NC
Bài tập 26 trang 29 SGK Hình học 11 NC
Bài tập 27 trang 29 SGK Hình học 11 NC
Bài tập 28 trang 29 SGK Hình học 11 NC