Bài tập 29 trang 29 SGK Hình học 11 NC

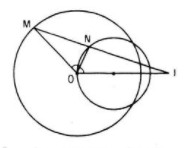
Đặt IO = d (d ≠ 0). Theo tính chất đường phân giác của tam giác MOI, ta có:

\(\begin{array}{*{20}{l}}
{\frac{{IN}}{{NM}} = \frac{{IO}}{{OM}} = \frac{d}{R}}\\
\begin{array}{l}
 \Rightarrow \frac{{IN}}{{IN + NM}} = \frac{d}{{d + R}}\\
 \Leftrightarrow \frac{{IN}}{{IM}} = \frac{d}{{d + R}}
\end{array}
\end{array}\)

Vì hai vecto \({\overrightarrow {IN} }\) và \({\overrightarrow {IM} }\) cùng hướng nên đẳng thức trên có nghĩa là: 

\(\overrightarrow {IN}  = \frac{d}{{d + R}}\overrightarrow {IM} \)

Nếu gọi V là phép vị tự tâm I tỉ số \(k = \frac{d}{{d + R}}\) thì V biến điểm M thành điểm N

Khi M ở vị trí M₀ trên đường tròn (O ; R) sao cho \(\widehat {IO{M_0}} = {0^ \circ }\) thì tia phân giác của góc \(\widehat {IO{M_0}}\) không cắt IM. Điểm N không tồn tại.

Vậy khi M chạy trên (O ; R) (M khác hẳn M₀) thì quỹ tích điểm N là ảnh của (O ; R) qua phép vị tự V bỏ đi ảnh của điểm M₀.

-- Mod Toán 11 HỌC247