Giải bài 1.25 tr 33 SBT Hình học 11
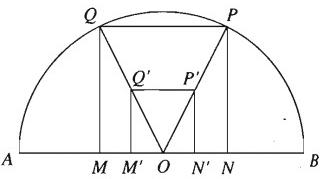
Cho nửa đường tròn đường kính AB. Hãy dựng hình vuông có hai đỉnh nằm trên nửa đường tròn, hai đỉnh còn lại nằm trên đường kính AB của nửa đường tròn đó.
Hướng dẫn giải chi tiết
Gọi O là trung điểm của AB. Giả sử dựng được hình vuông MNPQ có M, N thuộc đường kính AB, P, Q thuộc nửa đường tròn. Khi đó O phải là trung điểm của MN. Nếu lấy một hình vuông M′N′P′Q′ sao cho M′, N′ thuộc AB, O là trung điểm của M′N′ khi đó ta thấy \(\frac{{OM}}{{OM'}} = \frac{{ON}}{{ON'}} = \frac{{OQ}}{{OQ'}}\)
Từ đó suy ra hình vuông MNPQ là ảnh của hình vuông M′N′P′Q′ qua phép vị tự tâm O, suy ra O, P, P′ và O, Q, Q′ thẳng hàng.
Vậy ta có cách dựng: Dựng hình vuông M′N′P′Q′ nằm trong nửa hình tròn đã cho sao cho M′N′ thuộc AB và O là trung điểm của M′N′. Tia OP′ cắt nửa đường tròn tại P; tia OQ′ cắt nửa đường tròn tại Q .
Khi đó dễ thấy tứ giác MNPQ là hình vuông cần dựng.
-- Mod Toán 11 HỌC247
-


Tìm ảnh của đường tròn (C): \({\left( {x - 4} \right)^2} + {\left( {y + 1} \right)^2} = 1\) qua phép vị tự tâm O tỉ số k=2.
bởi Lê Bảo An
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng Oxy hai điểm A(4;5) và I(3;-2). Tìm ảnh của điểm A qua phép vị tự tâm I tỉ số k=3.
bởi Nguyễn Lệ Diễm
 31/05/2020
Theo dõi (0) 1 Trả lời
31/05/2020
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3 trang 29 SGK Hình học 11
Bài tập 1.24 trang 33 SBT Hình học 11
Bài tập 1.26 trang 33 SBT Hình học 11
Bài tập 1.23 trang 33 SBT Hình học 11
Bài tập 25 trang 29 SGK Hình học 11 NC
Bài tập 26 trang 29 SGK Hình học 11 NC
Bài tập 27 trang 29 SGK Hình học 11 NC
Bài tập 28 trang 29 SGK Hình học 11 NC