HOC247 xin gửi đến các em tóm tắt nội dung bài học "Đường thẳng vuông góc với mặt phẳng" trong môn Toán lớp 11. Thông qua bài học này, các em sẽ được tiếp cận với nhiều phương pháp chứng minh đường thẳng vuông góc với mặt phẳng trong không gian và áp dụng chúng vào giải các bài toán thực tế.
Tóm tắt lý thuyết
1.1. Đường thẳng vuông góc với mặt phẳng
Định nghĩa:
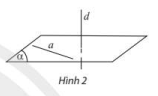
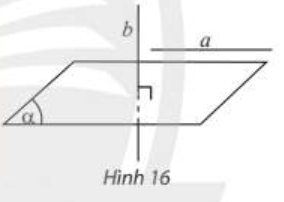
Đường thẳng d gọi là vuông góc với mặt phẳng (\(\alpha\)) nếu nó vuông góc với mọi đường thẳng ở nằm trong (\(\alpha\)), kí hiệu d \(\bot\) (\(\alpha\)).
Định lí 1:
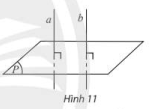
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (a) thì d \(\bot\) (a).
Có duy nhất một mặt phẳng đi qua một điểm và vuông góc với một đường thẳng cho trước. Có duy nhất một đường thẳng đi qua một điểm và vuông góc với một mặt phẳng cho trước.
1.2. Liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng
Định lí 3:
- Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thăng này thì cũng vuông góc với đường thăng kia.
- Hai đường thăng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Định lí 4:
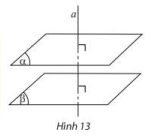
- Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
- Hai mặt phẳng phản biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Định lí 5:
- Cho đường thẳng a song song với mặt phẳng (\(\alpha\)). Đường thẳng nào vuông góc với (\(\alpha\)) thì cũng vuông góc với a.
- Nếu đường thẳng a và mặt phẳng (\(\alpha\)) (không chứa \(\alpha\)) cùng vuông góc với một đường thẳng b thì chúng song song với nhau
1.3. Phép chiếu vuông góc
Định nghĩa:
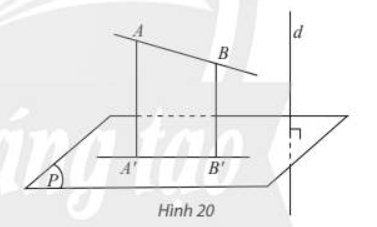
Cho mặt phẳng (P) và đường thẳng d vuông góc với (P). Phép chiếu song song theo phương của d lên mặt phẳng (P) được gọi là phép chiếu vuông góc lên (P).
Chú ý:
+) Phép chiếu vuông góc lên một mặt phẳng là một trường hợp đặc biệt của phép chiếu song song nên có đầy đủ các tính chất của phép chiếu song song.
+) Người ta còn dùng “phép chiếu lên (P)” thay cho phép chiếu vuông góc lên (P)” và dùng (H') là hình chiếu của (H) trên (P) thay cho (H') là hình chiếu vuông góc của (H) trên (P).
Định lí ba đường vuông góc
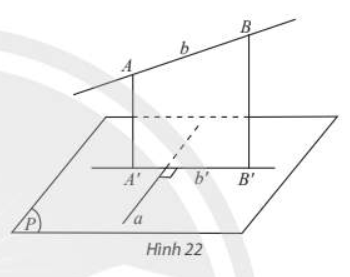
Cho đường thẳng a nằm trong mặt phẳng (P) và b là đường thẳng không nằm trong (P) và không vuông góc với (P). Gọi b' là hình chiếu vuông góc của ở trên (P). Khi đó a vuông góc với b khi và chỉ khi a vuông góc với b'.
Bài tập minh họa
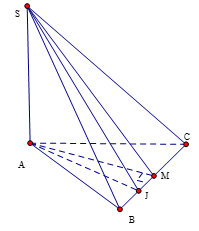
Câu 1. Cho hình chóp \(S.ABC\) có đáy là tam giác cân tại A,\(SA\) vuông góc với đáy, M là trung điểm của BC, J là trung điểm của \(BM\). Khẳng định nào sau đây đúng?
A. \(BC\bot \left( SAM \right)\). B. \(BC\bot \left( SAC \right)\). C. \(BC\bot \left( SAB \right)\). D. \(BC\bot \left( SAJ \right)\).
Hướng dẫn giải
Chọn A
\(SA\bot \left( ABC \right)\)\(\Rightarrow SA\bot BC\,\,\,\,\left( 1 \right)\).
\(\Delta ABC\) cân tại \(A\)\(\Rightarrow \)\(AM\bot BC\,\,\,\left( 2 \right)\).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có \(BC\bot \left( SAM \right)\).
Câu 2. Cho hình chóp \(S.ABCD\) có đáy là hình thoi tâm \(O\), \(SO\) vuông góc với mặt phẳng đáy. Gọi \(\alpha \) là góc giữa đường thẳng \(SD\) và mặt phẳng đáy. Khi đó
A. \(\alpha =\widehat{SDA}\). B. \(\alpha =\widehat{SDO}\). C. \(\alpha =\widehat{SAD}\). D. \(\alpha =\widehat{ASD}\).
Hướng dẫn giải
Chọn B
Ta có \(SO\bot \left( ABCD \right)\)\(\Rightarrow \)\(OD\) là hình chiếu vuông góc của \(SD\) lên mặt phẳng \(\left( ABCD \right)\).
Suy ra \(\left( \widehat{SD,\left( ABCD \right)} \right)=\left( \widehat{SD,SO} \right)=\widehat{SDO}\).
Vậy\(\alpha =\widehat{SDO}\).
Luyện tập Bài 2 Toán 11 Chân Trời Sáng Tạo
Học xong bài học này, em có thể:
– Giải thích được mối liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng.
– Nhận biết được khái niệm phép chiếu vuông góc.
3.1. Trắc nghiệm Bài 2 Toán 11 Chân Trời Sáng Tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Chân trời sáng tạo Chương 8 Bài 2 cực hay có đáp án và lời giải chi tiết.
-
- A. Nếu \(\left( P \right)\text{//}\left( Q \right)\) và \(b\bot \left( P \right)\) thì \(b\bot \left( Q \right)\).
- B. Nếu \(a\text{//}\left( P \right)\) và \(b\bot a\) thì \(b\bot \left( P \right)\).
- C. Nếu \(a\text{//}\left( P \right)\) và \(b\bot \left( P \right)\) thì \(b\bot a\)
- D. Nếu \(a\bot \left( P \right)\) và \(b\bot \left( P \right)\) thì \(a\text{//}b\).
-
- A. 4
- B. 3
- C. 2
- D. 1
-
- A. \(BC\bot \left( SAM \right)\).
- B. \(BC\bot \left( SAC \right)\).
- C. \(BC\bot \left( SAB \right)\).
- D. \(BC\bot \left( SAJ \right)\).
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 2 Toán 11 Chân Trời Sáng Tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 8 Bài 2 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 56 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 1 trang 57 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 2 trang 57 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 3 trang 58 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 1 trang 59 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 1 trang 59 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 4 trang 60 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 2 trang 61 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 3 trang 62 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 2 trang 62 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 5 trang 62 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 4 trang 63 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 6 trang 63 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Thực hành 5 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Vận dụng 3 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 64 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST
Bài tập 1 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 2 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 3 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Bài tập 4 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo - CTST
Hỏi đáp Bài 2 Toán 11 Chân Trời Sáng Tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247