Bài tập 3 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo
Cho tứ diện ABCD có DA ⊥ (ABC), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ AH ⊥ MD tại H.
a) Chứng minh rằng AH ⊥ (BCD).
b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng GK ⊥ (ABC).
Hướng dẫn giải chi tiết Bài tập 3
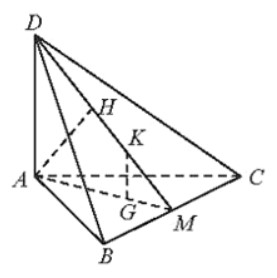
a) Tam giác ABC cân tại A.
Trung tuyến AM ⊥ BC.
Lại có DA ⊥ (ABC) DA ⊥ BC.
BC ⊥ (ADM) BC ⊥ AH. (1)
Theo giả thiết: AH ⊥ DM. (2)
Từ (1) và (2) suy ra AH ⊥ (BCD).
b)Ta có: nên GK // AD (theo định lí Thalès).
Ta lại có AD ⊥ (ABC) suy ra GK ⊥ (ABC).
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





