Bài tập 2 trang 55 SBT Toán 11 Tập 2 Chân trời sáng tạo
Cho tứ diện ABCD có AB ⊥ CD và AC ⊥ BD. Gọi H là hình chiếu vuông góc của A xuống mặt phẳng (BCD). Chứng minh rằng H là trực tâm của ∆BCD và AD ⊥ BC?
Hướng dẫn giải chi tiết Bài tập 2
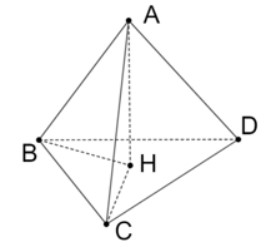
Theo giả thiết: \(\left\{ \begin{matrix} AH\bot CD \\ AB\bot CD \\ \end{matrix} \right.\)
Suy ra CD ⊥ AHB.
Do đó CD ⊥ BH. (1)
Chứng minh tương tự: CH ⊥ BD. (2)
Từ (1) và (2) suy ra H là trực tâm của ∆BCD.
Do đó DH ⊥ BC.
Lại có AH ⊥ BC suy ra BC ⊥ (AHD).
Vậy H là trực tâm của ∆BCD và AD ⊥ BC.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





