Thực hành 1 trang 95 SGK Toán 10 Chân trời sáng tạo tập 1
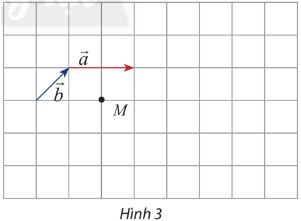
Cho hai vectơ cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) và điểm M như hình 3.
a) Hãy vẽ vectơ \(\overrightarrow {MN} = 3\overrightarrow a ,\overrightarrow {MP} = - 3\overrightarrow b \)
b) Cho biết mỗi ô có cạnh bằng 1. Tính: \(\left| {3\overrightarrow b } \right|,\left| { - 3\overrightarrow b } \right|,\left| {2\overrightarrow a + 2\overrightarrow b } \right|\).
Hướng dẫn giải chi tiết Thực hành 1
Phương pháp giải
Bước 1: Xác định hướng của vectơ \(\overrightarrow a ;\overrightarrow b \)
Bước 2: Xác định tỉ lệ độ dài \(\frac{{\left| {\overrightarrow x } \right|}}{{\left| {\overrightarrow a } \right|}}\)
Lời giải chi tiết
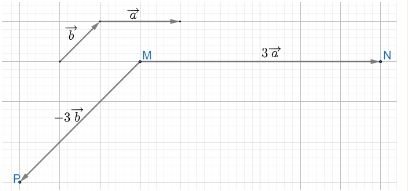
a) \(\overrightarrow {MN} = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)
Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải
\(\overrightarrow {MP} = - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)
Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái
b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:
\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right|\)
Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c = \overrightarrow a + \overrightarrow b \)
Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)} = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)} = \sqrt {10} \)
\( \Rightarrow \left| {2\overrightarrow a + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)
-- Mod Toán 10 HỌC247
-


Gọi \(G\) là trọng tâm tam giác \(ABC\). Đặt \(\overrightarrow a = \overrightarrow {GA} \) và \(\overrightarrow b = \overrightarrow {GB} \). Em hãy biểu thị mỗi vec tơ \(\overrightarrow {AB} ,\overrightarrow {GC} ,\overrightarrow {BC} ,\overrightarrow {CA} \) qua các vec tơ \(\overrightarrow a \) và \(\overrightarrow b \).
bởi Khanh Đơn
 04/09/2022
Theo dõi (0) 1 Trả lời
04/09/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Hoạt động khám phá 1 trang 94 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 96 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST