Thực hành 3 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1
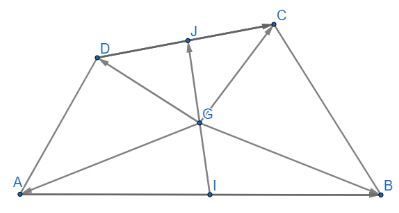
Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Chứng minh ba điểm I, G, J thẳng hàng
Hướng dẫn giải chi tiết Thực hành 3
Phương pháp giải
Sử dụng tính chất trung điểm và quy tắc ba điểm
\(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GI} \) với I là trung điểm AB
\(\overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0 \Leftrightarrow\) G là trung điểm IJ.
Lời giải chi tiết
Ta có:
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {GI} + \overrightarrow {IA} } \right) + \left( {\overrightarrow {GI} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JC} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {GI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) + 2\overrightarrow {GJ} + \left( {\overrightarrow {JC} + \overrightarrow {JD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {GI} + 2\overrightarrow {GJ} = \overrightarrow 0 \Leftrightarrow 2\left( {\overrightarrow {GI} + \overrightarrow {GJ} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0 \Rightarrow \)G là trung điểm của đoạn thẳng IJ
Vậy I, G, J thẳng hàng
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Vận dụng trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 96 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST