Hoạt động khám phá 5 trang 68 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST

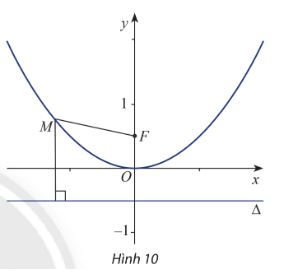
Trong mặt phẳng Oxy, cho điểm \(F\left( {0;\frac{1}{2}} \right)\), đường thẳng \(\Delta :y + \frac{1}{2} = 0\) và điểm \(M(x;y)\). Để tìm hệ thức giữa x và y sao cho \(M\) cách đều  F và \(\Delta \), một học sinh đã làm như sau:

+) Tính MF và MH (với H là hình chiếu của M trên \(\Delta \)):

\(MF = \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}} ,MH = d\left( {M,\Delta } \right) = \left| {y + \frac{1}{2}} \right|\)

+) Điều kiện để M cách đều F  và \(\Delta \):

\(\begin{array}{l}MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - \frac{1}{2}} \right)}^2}}  = \left| {y + \frac{1}{2}} \right|\\ \Leftrightarrow {x^2} + {\left( {y - \frac{1}{2}} \right)^2} = {\left( {y + \frac{1}{2}} \right)^2}\\ \Leftrightarrow {x^2} = 2y \Leftrightarrow y = \frac{1}{2}{x^2}\left( * \right)\end{array}\)

Hãy cho biết tên đồ thị (P) của hàm số (*) vừa tìm được.