Giải Bài 5 trang 76 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST

Phương pháp giải

Phương trình Hypebol có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\) có hai tiêu điểm \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\)và có tiêu cự là \(2c\) với \(c = \sqrt {{a^2} + {b^2}} \)

Lời giải chi tiết

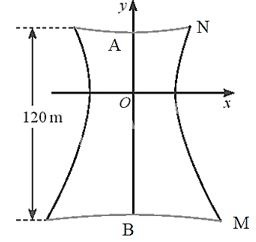
Ta có: O(0;0) là tâm đối xứng của hypebol

=> khoảng cách từ nóc tháp đến tâm đối xứng là OA, khoảng cách từ tâm đối xứng đến đáy là OB và \(OA = \frac{1}{2}OB\)

Mà chiều cao tháp là 120m hay \(OA + OB = 120\)\( \Rightarrow OA = 40(m);OB = 80(m)\)

Gọi r và R lần lượt là bán kính nóc và bán kính đáy của tháp.

Lấy N là điểm trên nóc tháp, thuộc vào hypebol \( \Rightarrow N\left( {r;40} \right)\)

Tương tự,  M là điểm ở đáy tháp, thuộc vào hypebol \( \Rightarrow M\left( {R; - 80} \right)\)

Thay tọa độ điểm \(M\left( {R; - 80} \right),N\left( {r;40} \right)\) vào phương trình hypebol ta tính được:

\(R = 30\sqrt {1 + \frac{{{{\left( { - 80} \right)}^2}}}{{{{50}^2}}}}  \approx 57\left( m \right),r = 30\sqrt {1 + \frac{{{{40}^2}}}{{{{50}^2}}}}  \approx 38\left( m \right)\)

Vậy bán kính nóc là 38m, bán kính đáy là 57m.

-- Mod Toán 10 HỌC247