Hướng dẫn Giải bài tập Toán 10 Chân trời sáng tạo Bài tập cuối chương 3 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Giải bài 1 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Tìm tập xác định của các hàm số sau:
a) \(y = 4{x^2} - 1\)
b) \(y = \dfrac{1}{{{x^2} + 1}}\)
c) \(y = 2 + \dfrac{1}{x}\)
-
Giải bài 2 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai:
a) \(y = (1 - 3m){x^2} + 3\)
b) \(y = (4m - 1){(x - 7)^2}\)
c) \(y = 2({x^2} + 1) + 11 - m\)
-
Giải bài 3 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vẽ đồ thị các hàm số sau:
a) \(y = {x^2} - 4x + 3\)
b) \(y = - {x^2} - 4x + 5\)
c) \(y = {x^2} - 4x + 5\)
d) \(y = - {x^2} - 2x - 1\)
-
Giải bài 4 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30 km/h.
a) Hãy biểu thị quãng đường s (tính bằng kilômét) mà người này đi được sau t phút bằng một hàm số.
b) Vẽ đồ thị biểu diễn hàm số s theo t.
-
Giải bài 5 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Biết rằng hàm số \(y = 2{x^2}{\rm{ + }}mx + n\) giảm trên khoảng \(\left( { - \infty ;1} \right),\)tăng trên khoảng \(\left( {1; + \infty } \right)\) và có tập giá trị là \([9; + \infty )\). Xác định giá trị của m và n.
-
Giải bài 6 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
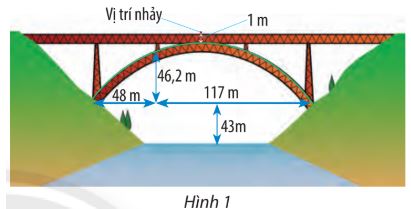
Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước). Chiếc cầu trong Hình 1 có bộ phận chống đỡ dạng parabol. Một người muốn thực hiện một cú nhày bungee từ giữa cầu xuống với dây an toàn. Người này cần trang bị sợi dây an toàn dài bao nhiêu mét? Biết rằng chiều dài của sợi dây đó bằng một phần ba khoảng cách từ vị trí bắt đầu nhảy đến mặt nước.
-
Giải bài 7 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
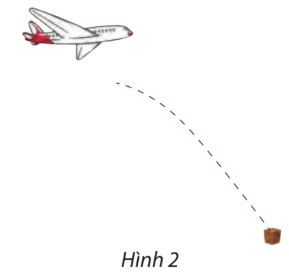
Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80 m, lúc đó máy bay đang bay với vận tốc 50 m/s. Để thùng hàng cứu trợ rơi đúngvị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí nào? Biết rằng nếu chọn gốc toạ độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì toạ độ của hàng cứu trợ được cho bởi hệ sau:
\(\left\{ \begin{array}{l}x = {v_0}t\\y = h - \frac{1}{2}g{t^2}\end{array} \right.\)
Trong đó, \({v_0}\) là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.
Lưu ý: Chuyển động này được xem là chuyển động ném ngang.
-
Giải bài 1 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Một hàm số có thể được cho bằng:
A. Bảng giá trị của hàm số
B. Đồ thị của hàm số
C. Công thức của hàm số
D. Tất cả đều đúng
-
Giải bài 2 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho hàm số \(y = f\left( x \right) = 2\left( {x + 1} \right)\left( {x - 3} \right) + 2x - 6\). Giá trị của hàm số khi x=3 là:
A. 8
B. 0
C. -6
D. 3
-
Giải bài 3 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Hàm số \(y = f\left( x \right) = \sqrt {x - 1} + \frac{1}{{{x^2} - 9}}\) có tập xác định là:
A. \(D = \left[ {1; + \infty } \right)\)
B. \(D = \mathbb{R}\backslash \left\{ { - 3;3} \right\}\)
C. \(D = \left[ {1; + \infty } \right)\backslash \left\{ 3 \right\}\)
D. \(D = \left[ {3; + \infty } \right)\)
-
Giải bài 4 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Hàm số nào trong các hàm số sau đây không phải là hàm số bậc hai?
A. \(y = f\left( x \right) = \sqrt 3 {x^2} + x - 4\)
B. \(y = f\left( x \right) = {x^2} + \frac{1}{x} - 5\)
C. \(y = f\left( x \right) = - 2x\left( {x - 1} \right)\)
D. \(y = f\left( x \right) = 2\left( {{x^2} + 1} \right) + 3x - 1\)
-
Giải bài 5 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Tập giá trị của hàm số \(y = f\left( x \right) = - 2{x^2} + \sqrt 2 x + 1\) là:
A. \(T = \left( { - \frac{5}{4}; + \infty } \right)\)
B. \(T = \left[ { - \frac{5}{4}; + \infty } \right)\)
C. \(T = \left( { - \infty ;\frac{5}{4}} \right)\)
D. \(T = \left( { - \infty ;\frac{5}{4}} \right]\)
-
Giải bài 6 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Hàm số \(y = f\left( x \right) = - \left( {x + 2} \right)\left( {x - 4} \right)\) đồng biến trên khoảng
A. \(\left( { - \infty ; - 1} \right)\)
B. \(\left( {1; + \infty } \right)\)
C. \(\left( { - \infty ;1} \right)\)
D. \(\left( { - 1; + \infty } \right)\)
-
Giải bài 7 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Hàm số \(y = f\left( x \right) = \left( {x + 2} \right)\left( {x - 2} \right)\) có:
A. Giá trị nhỏ nhất là 4
B. Giá trị lớn nhất là 4
C. Giá trị lớn nhất là \( - 4\)
D. Giá trị nhỏ nhất là \( - 4\)
-
Giải bài 8 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Để hàm số \(y = f\left( x \right) = \left( {m - 2} \right){\left( {x + 5} \right)^2} + \left( {{m^2} - 4} \right)\left| {x - 7} \right| + 3\) là một hàm số bậc hai thì giá trị của m là:
A. \(2\)
B. \(2\) hay \( - 2\)
C. \( - 2\)
D. \(4\)
-
Giải bài 9 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Đồ thị hàm số \(y = f\left( x \right) = - {x^2} + 4\left( {5m + 1} \right)x + \left( {3 - 2m} \right)\) có trục đối xứng là đường thẳng \(x = - 2\) khi m có giá trị là:
A. \( - 3\)
B. \( - \frac{2}{5}\)
C. \(\frac{3}{2}\)
D. \( - \frac{1}{5}\)
-
Giải bài 10 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
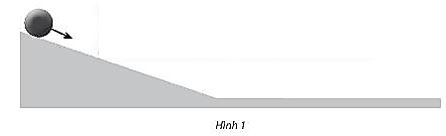
Một viên bi được thả không vận tốc đầu và lăn trên máng nghiêng như hình 1
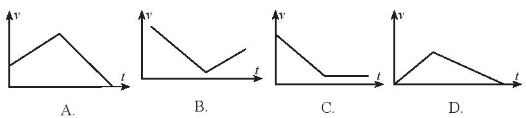
Đồ thị nào sau đây phù hợp với sự thay đổi vận tốc của viên bi theo thời gian?
-
Giải bài 1 trang 58 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Ta có bảng giá trị của hàm cầu đối với sản phẩm A theo đơn giá của sản phẩm A như sau:
Đơn giá sản phẩm A (đơn vị: Nghìn đồng)
10
20
40
70
90
Lượng cầu (nhu cầu về số sản phẩm)
338
288
200
98
50
a) Giả sử hàm cầu là một hàm số bậc hai theo đơn giá x , hãy viết công thức của hàm này, biết rằng \(c = 392\)
b) Chứng tỏ rằng hàm số có thể viết thành dạng \(y = f\left( x \right) = a{\left( {b - x} \right)^2}\)
c) Giả sử hàm cầu này lấy mọi giá trị trên đoạn \(\left[ {0;100} \right]\), hãy tính lượng cầu khi đơn giá sản phẩm A là 30, 50, 100
d) Cùng giả thiết với câu c) nếu lượng cầu là 150 sản phẩm thì đơn giá sản phẩm A là khoảng bao nhiêu (đơn vị: nghìn đồng)
-
Giải bài 2 trang 58 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Khi một vật từ vị trí \({y_0}\) được ném xiên lên cao theo góc \(\alpha \) (so với phương ngang) với vận tốc ban đầu \({v_0}\) thì phương trình chuyển động của vật này là:
\(y = \frac{{ - g{x^2}}}{{2v_0^2{{\cos }^2}\alpha }} + \tan \alpha .x + {y_0}\)
a) Vật bị ném xiên như vậy có chuyển động theo đường xiên không? Tại sao?
b) Giả sử góc ném có số đo là \(45^\circ \), vận tốc ban đầu của vật là \(3\)m/s và vật được ném xiên từ độ cao 1 m so với mặt đất, hãy viết phương trình chuyển động của vật
c) Một vận động viên ném lao đã lập kỉ lục với độ xa 90 m. Biết người này ném lao từ độ cao 0,9 m và góc ném là khoảng \(45^\circ \). Hỏi vận tốc đầu của lao khi được ném đi là bao nhiêu?
(Lưu ý: Lấy giá trị \(g = 10\) m/s2 cho gia tốc trọng trường và làm tròn kết quả đến 2 chữ số thập phân)