Giải bài 5 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1
Biết rằng hàm số \(y = 2{x^2}{\rm{ + }}mx + n\) giảm trên khoảng \(\left( { - \infty ;1} \right),\)tăng trên khoảng \(\left( {1; + \infty } \right)\) và có tập giá trị là \([9; + \infty )\). Xác định giá trị của m và n.
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải
Từ tập giá trị suy ra GTNN của hàm số bằng 9.
Lập bảng biến thiên, xác định giá trị nhỏ nhất của hàm số.
Lời giải chi tiết
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - m}}{{2.2}} = - \frac{m}{4};{y_S} = f( - \frac{m}{4})\)
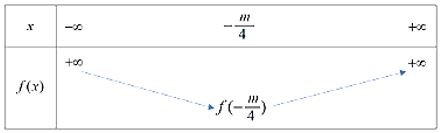
Vì hàm số bậc hai có \(a = 2 > 0\) nên ta có bảng biến thiên sau:
Hàm số đạt giá trị nhỏ nhất bằng \(f( - \frac{m}{4}).\)
Hàm số giảm trên \(( - \infty ; - \frac{m}{4})\) và tăng trên \(( - \frac{m}{4}; + \infty )\)
Theo giả thiết, ta có:
Hàm số giảm trên khoảng \(\left( { - \infty ;1} \right)\)\( \Rightarrow \left( { - \infty ;1} \right) \subset ( - \infty ; - \frac{m}{4}) \Leftrightarrow 1 \le - \frac{m}{4}.\)
Tương tự hàm số tăng trên khoảng \(\left( {1; + \infty } \right)\)\( \Rightarrow \left( {1; + \infty } \right) \subset ( - \frac{m}{4}; + \infty ) \Leftrightarrow - \frac{m}{4} \le 1.\)
Do đó: \( - \frac{m}{4} = 1\) hay \(m = - 4\)
Lại có: Tập giá trị là \([9; + \infty )\)\( \Rightarrow \)Giá trị nhỏ nhất của hàm số bằng 9.
\( \Leftrightarrow f(1) = f( - \frac{m}{4}) = 9 \Leftrightarrow {2.1^2} - ( - 4).1 + n = 9 \Leftrightarrow n = 3.\)
Vậy \(m = - 4,n = 3.\)
-- Mod Toán 10 HỌC247
-


Thực hiện tìm tập xác định của các hàm số: \(y = \sqrt {2 - 3x} - {1 \over {\sqrt {1 - 2x} }}\)
bởi Nguyễn Hạ Lan
 28/08/2022
Theo dõi (0) 1 Trả lời
28/08/2022
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Giải bài 3 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 59 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 56 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 57 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 58 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 58 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST