Câu hỏi trắc nghiệm (50 câu):
-
Câu 1: Mã câu hỏi: 465095
Trong không gian \(Oxyz\), cho 2 điểm \(A\left( -2\,;-1\,;\,3 \right)\) và \(B\left( 0\,;\,3\,;\,1 \right)\). Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của đoạn \(AB\). Một vec tơ pháp tuyến của \(\left( \alpha \right)\) có tọa độ là?
- A. \(\,\overrightarrow{n}=\left( 2\,;\,4\,;-1 \right)\).
- B. \(\,\overrightarrow{n}=\left( 1\,;\,0\,;\,1 \right)\).
- C. \(\,\overrightarrow{n}=\left( -1\,;\,1\,;\,2 \right)\).
- D. \(\,\overrightarrow{n}=\left( 1\,;\,2\,;-1 \right)\).
-
Câu 2: Mã câu hỏi: 465096
Tập nghiệm của phương trình sau \({{\log }_{2}}x+{{\log }_{4}}x+{{\log }_{16}}x=7\) là?
- A. \(\text{ }\!\!\{\!\!\text{ }16\}\).
- B. \(\text{ }\!\!\{\!\!\text{ }\sqrt{2}\}\).
- C. \(\text{ }\!\!\{\!\!\text{ }4\}\).
- D. \(\text{ }\!\!\{\!\!\text{ 2}\sqrt{2}\}\).
-
Câu 3: Mã câu hỏi: 465097
Cho mặt cầu \(\left( S \right)\) có diện tích bằng \(4\pi \). Tính thể tích khối cầu \(\left( S \right)\)?
- A. \(16\pi \).
- B. \(32\pi \).
- C. \(\frac{4\pi }{3}\).
- D. \(\frac{16\pi }{3}\).
-
Câu 4: Mã câu hỏi: 465099
Cho hàm số \(f\left( x \right)\) có đồ thị như hình dưới. Giá trị cực tiểu của hàm số bằng?
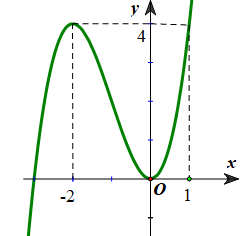
- A. 0
- B. -2
- C. 4
- D. 1
-
Câu 5: Mã câu hỏi: 465124
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình sau:
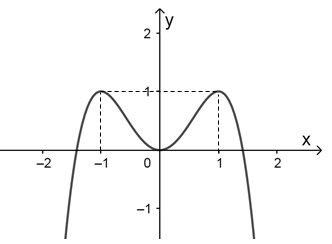
Mệnh đề nào sau đây đúng về hàm số đó?
- A. Nghịch biến trên khoảng \(\left( -1\,;\,\,1 \right)\).
- B. Đồng biến trên khoảng \(\left( 0\,;\,+\infty \right)\).
- C. Đồng biến trên khoảng \(\left( 0\,;\,1 \right)\).
- D. Nghịch biến trên khoảng \(\left( -\infty \,;\,0 \right)\).
-
Câu 6: Mã câu hỏi: 465132
Cho khối lập phương có độ dài đường chéo bằng \(\sqrt{3}\). Tính thể tích khối lập phương đó?
- A. \(64\).
- B. \(27\).
- C. \(8\).
- D. \(1\).
-
Câu 7: Mã câu hỏi: 465136
Họ nguyên hàm của hàm số sau đây \(f\left( x \right)=\frac{1}{x}\) là?
- A. \(-\frac{1}{{{x}^{2}}}\).
- B. \(\ln x+C\).
- C. \(\ln \left| x \right|+C\).
- D. \(-\frac{1}{{{x}^{2}}}+C\).
-
Câu 8: Mã câu hỏi: 465138
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\frac{x}{2}=\frac{y}{1}=\frac{z-1}{2}\). VTCP của \(d\) là?
- A. \(\overrightarrow{u}=\left( 2;\,\,1;\,\,2 \right).\)
- B. \(\overrightarrow{u}=\left( 0;\,\,0;\,\,1 \right).\)
- C. \(\overrightarrow{u}=\left( 2;\,\,6;\,\,2 \right).\)
- D. \(\overrightarrow{u}=\left( 0;\,\,0;\,\,-1 \right).\)
-
Câu 9: Mã câu hỏi: 465141
Cho CSN \(\left( {{u}_{n}} \right)\) có \({{u}_{1}}=1,\,\,{{u}_{2}}=-2\). Giá trị của \({{u}_{2019}}\) bằng?
- A. \({{u}_{2019}}=-{{2}^{2018}}\).
- B. \({{u}_{2019}}={{2}^{2018}}\).
- C. \({{u}_{2019}}=-{{2}^{2019}}\).
- D. \({{u}_{2019}}={{2}^{2019}}\).
-
Câu 10: Mã câu hỏi: 465143
Môđun của số phức sau đây \(z=(-4+3i).i\) bằng?
- A. \(\sqrt{7}.\)
- B. 5
- C. 3
- D. 4
-
Câu 11: Mã câu hỏi: 465147
Cho biết \(\int\limits_{0}^{1}{f(x)\text{d}x}=-3\) và \(\int\limits_{0}^{1}{g(x)\text{d}x}=2\), khi đó \(\int\limits_{0}^{1}{\left[ f\left( x \right)+2g\left( x \right) \right]\text{d}x}\) bằng?
- A. \(1\).
- B. \(-1\).
- C. \(-7\).
- D. \(5\).
-
Câu 12: Mã câu hỏi: 465149
Tập nghiệm của BPT \({{\log }_{2}}\left( 4x+8 \right)-{{\log }_{2}}x\le 3\) là?
- A. \(\left( -\infty ;2 \right].\)
- B. \(\left[ 3;+\infty \right).\)
- C. \(\left[ 2;+\infty \right).\)
- D. \(\left[ 1;+\infty \right).\)
-
Câu 13: Mã câu hỏi: 465161
Cho số phức \(z\) thỏa mãn \(z+2i.\overline{z}=1+17i\). Khi đó giá trị của \(\left| z \right|\) bằng?
- A. \(\left| z \right|=6\).
- B. \(\left| z \right|=\sqrt{146}\).
- C. \(\left| z \right|=10\).
- D. \(\left| z \right|=\sqrt{58}\).
-
Câu 14: Mã câu hỏi: 465163
Hàm số sau \(y=f\left( x \right)\) có đạo hàm \(f'\left( x \right)=\left( {{x}^{4}}-{{x}^{2}} \right){{\left( x+2 \right)}^{3}},\forall x\in \mathbb{R}\). Số điểm cực trị của hàm số là?
- A. 3
- B. 2
- C. 1
- D. 4
-
Câu 15: Mã câu hỏi: 465166
Đường cong trong hình bên là đồ thị của hàm số nào?
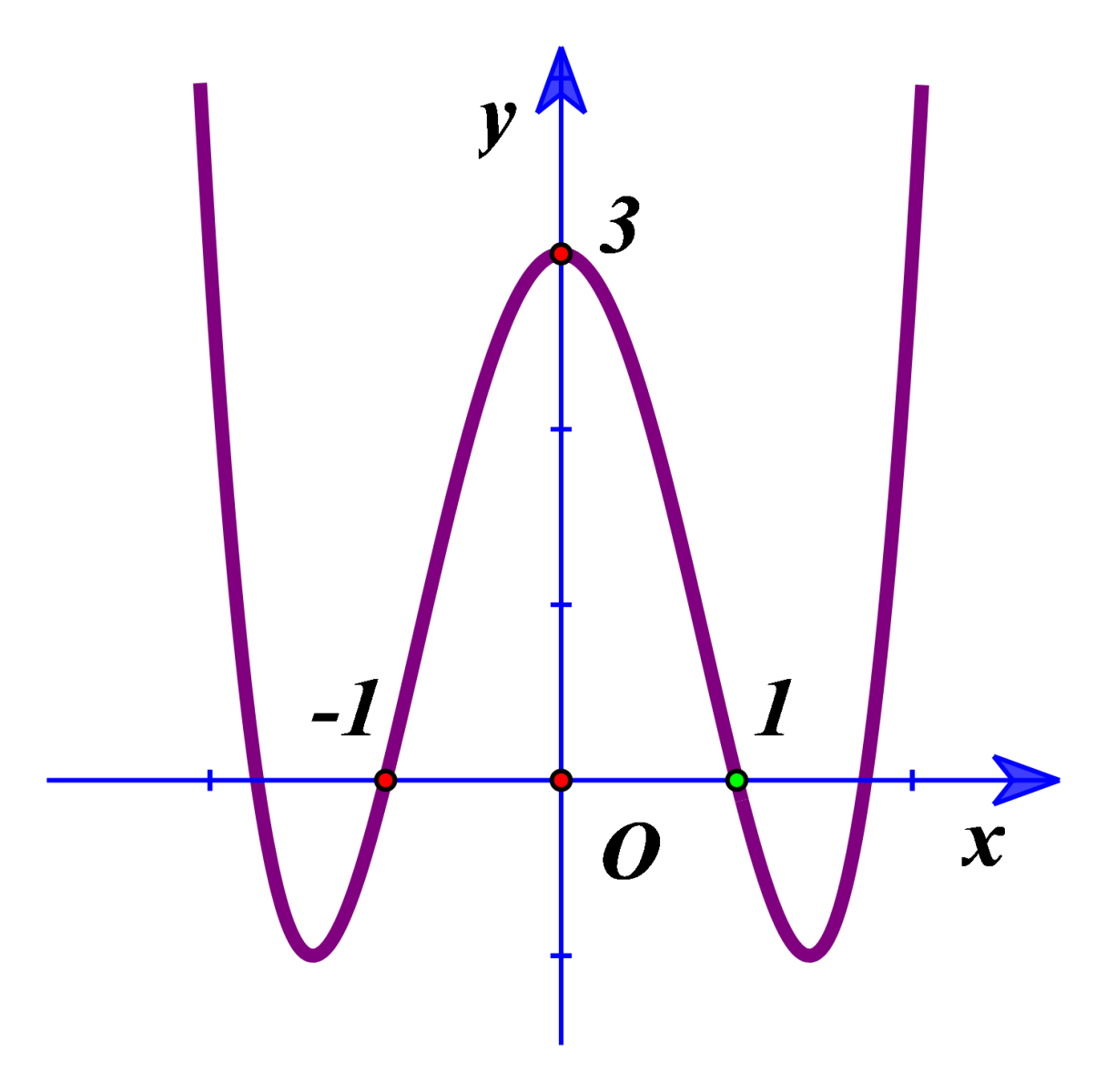
- A. \(y={{x}^{4}}+4{{x}^{2}}-5\).
- B. \(y={{x}^{3}}+4{{x}^{2}}+3\).
- C. \(y={{x}^{4}}-4{{x}^{2}}+3\).
- D. \(y=-{{x}^{4}}+4{{x}^{2}}+3\).
-
Câu 16: Mã câu hỏi: 465168
Trong không gian \(Oxyz\), khoảng cách giữa \(\left( P \right):x+2y+2z=0\) & \(\left( Q \right):x+2y+2z-12=0\) bằng?
- A. 2
- B. 3
- C. 1
- D. 4
-
Câu 17: Mã câu hỏi: 465175
Trong không gian \(Oxyz\), mặt cầu có tâm \(I\left( -1;2;-3 \right)\) và đi qua điểm \(A\left( 2;0;0 \right)\) có phương trình là?
- A. \({{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=22\).
- B. \({{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+3 \right)}^{2}}=11\).
- C. \({{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=22\).
- D. \({{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+3 \right)}^{2}}=22\).
-
Câu 18: Mã câu hỏi: 465180
Tìm tham số \(m\) để ĐTHS \(y=\frac{\left( m+1 \right)x-5m}{2x-m}\) có tiệm cận ngang là đường thẳng \(y=1\)?
- A. \(m=-1\).
- B. \(m=\frac{1}{2}\).
- C. \(m=2\).
- D. \(m=1\).
-
Câu 19: Mã câu hỏi: 465184
Diện tích hình phẳng giới hạn bởi đồ thị của các HS \(y=2{{x}^{2}}+x+1\) và \(y={{x}^{2}}+3\) bằng?
- A. \(\frac{9}{2}.\)
- B. \(\frac{5}{2}.\)
- C. \(4.\)
- D. \(2.\)
-
Câu 20: Mã câu hỏi: 465190
Ký hiệu \({{z}_{1}},\text{ }{{z}_{2}}\) là 2 nghiệm phức của pt \({{z}^{2}}+2z+11=0\). Khi đó giá trị biểu thức \(A={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}\) bằng?
- A. \(2\sqrt{11}\).
- B. \(22\).
- C. \(11\).
- D. \(24\).
-
Câu 21: Mã câu hỏi: 465194
Cho hình chóp tứ giác \(S.ABCD\) có \(SA=SB=SC=SD=4\sqrt{11}\) và đáy \(ABCD\) là hình vuông cạnh \(8\). Thể tích của khối chóp \(S.ABC\) bằng?
- A. \(256\).
- B. \(32\).
- C. \(128\).
- D. \(64\).
-
Câu 22: Mã câu hỏi: 465200
Cho 2 số thực \(a\),\(b\) thoả mãn \(2{{\log }_{3}}\left( a-2b \right)={{\log }_{3}}a+{{\log }_{3}}b\) và \(a>2b>0\). Khi đó \(\frac{a}{b}\) bằng?
- A. 1
- B. 2
- C. 3
- D. 5
-
Câu 23: Mã câu hỏi: 465202
Tìm họ nguyên hàm của hàm số sau \(f\left( x \right)=x.\sin 2x\) là?
- A. \(-\frac{1}{2}\cos 2x+\frac{1}{4}\sin 2x\).
- B. \(-\frac{x}{2}\cos 2x+\frac{1}{4}\sin 2x+C\).
- C. \(-\frac{1}{2}\cos 2x+\frac{1}{4}\sin 2x+C\)
- D. \(\frac{x}{2}\cos 2x+\frac{1}{4}\sin 2x\).
-
Câu 24: Mã câu hỏi: 465205
Cho hàm số \(y={{x}^{3}}-3x+2\) có đồ thị như hình dưới. Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \({{x}^{3}}-3x+2-2m=0\) có 3 nghiệm thực phân biệt?
- A. \(0 < m < 4\).
- B. \(0 < m < 2\).
- C. \(0\le m\le 4\).
- D. \(0\le m\le 2\).
-
Câu 25: Mã câu hỏi: 465209
Tính tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó bằng?
- A. \(\frac{\pi \sqrt{3}}{2}\).
- B. \(\frac{2\sqrt{3}}{3\pi }\).
- C. \(\frac{3\sqrt{2}}{2\pi }\).
- D. \(\frac{\pi \sqrt{2}}{3}\).
-
Câu 26: Mã câu hỏi: 465212
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), cạnh \(SA\) vuông góc với mp đáy và \(SA=2a\), gọi \(M\) là trung điểm của \(SC\). Tính côsin của góc \(\alpha \) là góc giữa đường thẳng \(BM\) và \(\left( ABC \right)\)?
- A. \(\cos \alpha =\frac{\sqrt{7}}{14}\).
- B. \(\cos \alpha =\frac{2\sqrt{7}}{7}\).
- C. \(\cos \alpha =\frac{\sqrt{21}}{7}\).
- D. \(\cos \alpha =\frac{\sqrt{5}}{7}\).
-
Câu 27: Mã câu hỏi: 465241
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(\left( SAC \right)\bot \left( ABC \right)\) và \(AB=3a,\text{ }BC=5a\). Biết rằng \(SA=2a\sqrt{3}\) và \(\widehat{SAC}=30{}^\circ \). Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( SBC \right)\) bằng?
- A. \(\frac{3a\sqrt{17}}{4}\).
- B. \(\frac{6a\sqrt{7}}{7}\).
- C. \(\frac{3a\sqrt{7}}{14}\).
- D. \(\frac{12a}{5}\).
-
Câu 28: Mã câu hỏi: 465244
Tổng tất cả các nghiệm của phương trình sau \({{\log }_{2}}\left| {{x}^{2}}+2x-3 \right|-{{\log }_{2}}\left| x+3 \right|=3\) bằng?
- A. \(-2\).
- B. \(-4\).
- C. \(9\).
- D. \(2\).
-
Câu 29: Mã câu hỏi: 465247
Cho \(\int\limits_{1}^{3}{\frac{\ln x}{{{\left( x+1 \right)}^{2}}}\text{dx}}=\frac{a}{b}\ln 3-c\ln 2\) với \(a,\text{ }b,\text{ }c\in \mathbb{N}*\) và phân số \(\frac{a}{b}\) tối giản. Tính giá trị của \(a+b+c\)?
- A. 8
- B. 7
- C. 6
- D. 9
-
Câu 30: Mã câu hỏi: 465249
Cho số phức \(z\) thỏa mãn \(\left( 1-i \right)\overline{z}=5+i\). Cho biết số phức \(\text{w}=2z+i\) là?
- A. \(\text{w}=4-5i\).
- B. \(\text{w}=4+5i\).
- C. \(\text{w}=4+7i\).
- D. \(\text{w}=4-7i\).
-
Câu 31: Mã câu hỏi: 465250
Trong không gian \(Oxyz\), tam giác \(ABC\) với \(A\left( 3;-1;2 \right)\), \(B\left( -1;3;5 \right)\) và \(C\left( 3;1;-3 \right)\). Đường trung tuyến \(AM\) của \(\Delta ABC\) có phương trình là?
- A. \(\left\{ \begin{align} & x=1-2t \\ & y=2-3t \\ & z=1+t \\ \end{align} \right.\).
- B. \(\left\{ \begin{align} & x=1+2t \\ & y=2-3t \\ & z=1+t \\ \end{align} \right.\).
- C. \(\left\{ \begin{align} & x=1+2t \\ & y=2+3t \\ & z=1+t \\ \end{align} \right.\).
- D. \(\left\{ \begin{align} & x=3+2t \\ & y=-1+3t \\ & z=2+t \\ \end{align} \right.\).
-
Câu 32: Mã câu hỏi: 465257
Cho biết \(\int\limits_{-1}^{2}{f\left( x \right)}\text{d}x=2\) và \(\int\limits_{1}^{2}{f\left( x \right)}\text{d}x=5\), tích phân \(\int\limits_{1}^{2}{f\left( 3-2x \right)}\text{d}x\) bằng?
- A. \(3\).
- B. \(\frac{-3}{2}\).
- C. \(-3\).
- D. \(\frac{3}{2}\).
-
Câu 33: Mã câu hỏi: 465259
Cho hình nón có thiết diện qua trục là 1 tam giác cân có góc ở đỉnh bằng \({{120}^{0}}\), cạnh bên bằng \(2\). Chiều cao \(h\) của hình nón là?
- A. \(h=\sqrt{2}\).
- B. \(h=1\).
- C. \(h=\sqrt{3}\).
- D. \(h=\frac{\sqrt{2}}{2}\).
-
Câu 34: Mã câu hỏi: 465261
Trong không gian \(Oxyz\), cho điểm \(M\left( 2;1;1 \right)\), mp \(\left( \alpha \right):x+y+z-4=0\) và mặt cầu \(\left( S \right):{{\left( x-3 \right)}^{2}}+{{\left( y-3 \right)}^{2}}+{{\left( z-4 \right)}^{2}}=16\). Phương trình đường thẳng \(\Delta \) đi qua \(M\) và nằm trong \(\left( \alpha \right)\) cắt mặt cầu \(\left( S \right)\) theo một đoạn thẳng có độ dài nhỏ nhất. Đường thẳng \(\Delta \) đi qua điểm nào trong các điểm sau đây?
- A. \(\left( 4;-3;3 \right)\).
- B. \(\left( 4;-3;-3 \right)\).
- C. \(\left( 4;3;3 \right)\).
- D. \(\left( -4;-3;-3 \right)\)
-
Câu 35: Mã câu hỏi: 465262
Có tất cả bao nhiêu số phức \(z\) thỏa mãn \(3\left| z+\overline{z} \right|+2\left| z-\overline{z} \right|=12\) và \(\left| z+2-3i \right|=\left| \overline{z}-4+i \right|\)?
- A. 3
- B. 1
- C. 4
- D. 2
-
Câu 36: Mã câu hỏi: 465265
Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ:
Tập hợp tất cả giá trị thực của tham số \(m\) để phương trình \(f\left( 2\sin x+1 \right)=m\) có nghiệm thuộc nửa khoảng \(\left[ 0\,;\frac{\pi }{6} \right)\) là?
- A. \(\left( -2\,;0 \right]\).
- B. \(\left( 0\,;2 \right]\).
- C. \(\left[ -2\,;2 \right)\).
- D. \(\left( -2\,;0 \right)\).
-
Câu 37: Mã câu hỏi: 465266
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) cạnh bằng 1. Gọi \(M\) là trung điểm cạnh \(B{B}'\). Mặt phẳng \(\left( M{A}'D \right)\) cắt cạnh \(BC\) tại \(K\). Tính thể tích của khối đa điện \({A}'{B}'{C}'{D}'MKCD\)?
- A. \(\frac{7}{24}\).
- B. \(\frac{7}{17}\).
- C. \(\frac{1}{24}\).
- D. \(\frac{17}{24}\).
-
Câu 38: Mã câu hỏi: 465267
Tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số sau \(y={{x}^{3}}-3m{{x}^{2}}+3x-6{{m}^{3}}\) đồng biến trên khoảng \(\left( 0;\text{ }+\infty \right)\) là?
- A. \(\left( -\infty ;\text{ }1 \right].\)
- B. \(\left( -\infty ;\text{ }2 \right].\)
- C. \(\left( -\infty ;\text{ }0 \right].\)
- D. \(\left[ 2;\text{ }+\infty \right).\)
-
Câu 39: Mã câu hỏi: 465268
Cho một vật chuyển động chậm dần đều với vận tốc \(v(t)=180-20t\,\left( m/s \right)\). Tính quãng đường mà vật di chuyển được từ thời điểm \(t=0\,(~s\,)\) đến thời điểm mà vật dừng lại?
- A. \(810~m\).
- B. \(9~m\).
- C. \(180~m\).
- D. \(160~m\).
-
Câu 40: Mã câu hỏi: 465269
Tại SEA Games 2019, môn bóng chuyền nam có 8 đội bóng tham dự, trong đó có 2 đôi Việt Nam và Thái Lan. Các đội bóng được chia ngẫu nhiên thành 2 bảng có số đội bóng bằng nhau. Xác suất để hai đội Việt Nam và Thái Lan nằm hai bảng khác nhau bằng?
- A. \(\frac{3}{7}\).
- B. \(\frac{4}{7}\).
- C. \(\frac{3}{14}\).
- D. \(\frac{11}{14}\).
-
Câu 41: Mã câu hỏi: 465270
Trong không gian \(Oxyz\), cho hình lập phương \(ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\) biết \(A\left( 0\,;0\,;0 \right)\), \(B\left( 1\,;0\,;0 \right)\), \(D\left( 0\,;1\,;0 \right)\) và \({{A}_{1}}\left( 0\,;0\,;1 \right)\). Gọi \(\left( P \right)\text{:}\,\,ax+by+cz-3=0\) là phương trình mặt phẳng chứa \(C{{D}_{1}}\) và tạo với mặt phẳng \(\left( B{{B}_{1}}{{D}_{1}}D \right)\) một góc có số đo nhỏ nhất. Giá trị của \(T=a+b+c\) bằng?
- A. \(-1\).
- B. \(6\).
- C. \(4\).
- D. \(3\).
-
Câu 42: Mã câu hỏi: 465271
Trong không gian \(Oxyz\), cho \(A\left( 0\,;\,1\,;\,1 \right)\), \(B\left( 2\,;\,-1\,;\,1 \right)\), \(C\left( 4\,;\,1\,;\,1 \right)\) và \(\left( P \right)\,:\,x+\,y+z-6\,=\,0\). Xét điểm \(M\left( a\,;\,b\,;\,c \right)\) thuộc \(\left( P \right)\) sao cho \(\left| \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} \right|\) đạt GTNN. Giá trị của \(\,2a+4b+c\) bằng?
- A. 6
- B. 12
- C. 7
- D. 5
-
Câu 43: Mã câu hỏi: 465272
Gọi \(S\) là tập hợp tất cả các giá trị nguyên dương của tham số \(m\) để BPT \({{x}^{6}}+3{{x}^{4}}-{{m}^{3}}{{x}^{3}}+4{{x}^{2}}-mx+2\ge 0\) đúng với mọi \(x\in \left[ 1;3 \right]\). Tổng của tất cả các phần tử thuộc \(S\) bằng?
- A. 3
- B. 2
- C. 1
- D. 4
-
Câu 44: Mã câu hỏi: 465273
Cho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như hình dưới. Hàm số \(y={{e}^{3f\left( 2-x \right)+1}}+{{3}^{f\left( 2-x \right)}}\) đồng biến trên khoảng nào?
- A. \(\left( 1;+\infty \right)\).
- B. \(\left( -1;\text{3} \right)\).
- C. \(\left( -\infty ;-2 \right)\).
- D. \(\left( -2;1 \right)\).
-
Câu 45: Mã câu hỏi: 465274
Cho 1 chiếc cổng có dạng là một parabol \(\left( P \right)\) có kích thước như hình vẽ, biết chiều cao cổng bằng \(4\,m\,,\,AB\,=\,4\,m\). Người ta thiết kế cửa đi là một hình chữ nhật \(CDEF\,\), phần còn lại dùng để trang trí. Biết chi phí phần tô đậm là 1.000.000 đồng/\({{m}^{2}}\). Hỏi số tiền ít nhất dùng để trang trí phần tô đậm gần với số tiền nào dưới đây?
- A. 4.450.000 đồng.
- B. 4.605.000 đồng.
- C. 4.505.000 đồng.
- D. 4.509.000 đồng.
-
Câu 46: Mã câu hỏi: 465275
Cho số phức \(z=a+bi\) \(\left( a,\,b\,\in \mathbb{R} \right)\) thỏa mãn \(\left| z+4 \right|+\left| z-4 \right|=10\) và \(\left| z-6 \right|\) lớn nhất. Tính giá trị của \(S=a+b\)?
- A. 11
- B. -5
- C. -3
- D. 5
-
Câu 47: Mã câu hỏi: 465276
Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ 1\,;2 \right]\) thỏa mãn \(\int\limits_{1}^{2}{{{\left( x-1 \right)}^{2}}f\left( x \right)\text{d}x}=-\frac{1}{3}\), \(f\left( 2 \right)=0\) và \(\int\limits_{1}^{2}{{{\left[ {f}'\left( x \right) \right]}^{2}}\text{d}x}=7\). Tính tích phân của \(I=\int\limits_{1}^{2}{f\left( x \right)\text{d}x}\)?
- A. \(I=\frac{7}{5}\)
- B. \(I=-\frac{7}{5}\).
- C. \(I=-\frac{7}{20}\).
- D. \(I=\frac{7}{20}\).
-
Câu 48: Mã câu hỏi: 465277
Cho phương trình \({{3}^{x}}\left( {{3}^{2x}}+1 \right)-\left( {{3}^{x}}+m+2 \right)\sqrt{{{3}^{x}}+m+3}=2\sqrt{{{3}^{x}}+m+3}\), với \(m\) là tham số. Có tất cả bao nhiêu giá trị nguyên âm của \(m\) để phương trình có nghiệm thực?
- A. 5
- B. 3
- C. 6
- D. 4
-
Câu 49: Mã câu hỏi: 465278
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng 1. Biết k/c từ \(A\) đến mp \(\left( SBC \right)\) là \(\frac{\sqrt{6}}{4}\), từ \(B\) đến mặt phẳng \(\left( SAC \right)\) là \(\frac{\sqrt{15}}{10}\), từ \(C\) đến mặt phẳng \(\left( SAB \right)\) là \(\frac{\sqrt{30}}{20}\).và hình chiếu vuông góc của \(S\) xuống đáy nằm trong tam giác \(ABC\). Thể tích khối chóp \(S.ABC\) bằng?
- A. \(\frac{1}{36}\).
- B. \(\frac{1}{48}\).
- C. \(\frac{1}{12}\).
- D. \(\frac{1}{24}\).
-
Câu 50: Mã câu hỏi: 465279
Trong không gian với hệ tọa độ \(Oxyz,\) cho 2 điểm \(A\left( 2;1;3 \right),B\left( 6;5;5 \right)\). Gọi \(\left( S \right)\) là mặt cầu đường kính \(AB\). Mặt phẳng \(\left( P \right)\) vuông góc với \(AB\) tại \(H\) sao cho khối nón đỉnh \(A\) và đáy là hình tròn tâm \(H\) là giao tuyến của \(\left( S \right)\) và \(\left( P \right)\) có thể tích lớn nhất, biết rằng \(\left( P \right):2x+by+cz+d=0\) với \(b,c,d\in \mathbb{Z}\). Tính \(S=b+c+d\)?
- A. \(S=18.\)
- B. \(S=-18.\)
- C. \(S=-12.\)
- D. \(S=24.\)


.PNG)
.PNG)
.PNG)
.PNG)




