Câu 1: Công suất tỏa nhiệt trung bình của dòng điện xoay chiều được tính theo công thức nào sau đây?

      A. P = uicos\(\varphi\)                       B. P = uisin\(\varphi\)                    C. P = UIcos\(\varphi\)                    D. P = UIsin\(\varphi\)

Lời giải
\(P=U.I.cos\varphi =\frac{U_0I_0}{2}cos\varphi =R.I^2.cos^2\varphi\)Câu 2: Mạch điện nào sau đây có hệ số công suất nhỏ nhất?

      A. Điện trở thuần R₁ nối tiếp với điện trở thuần R₂.
      B. Điện trở thuần R nối tiếp cuộn cảm L.
      C. Điện trở thuần R nối tiếp tụ điện C.
      D. Cuộn cảm L nối tiếp với tụ điện C.

Lời giải
\(0\leq cos\varphi \leq 1, cos\varphi =\frac{R}{\sqrt{R^2+Z_L_C^2}}\)Câu 3: Mạch điện xoay chiều RLC mắc nối tiếp đang có tính cảm kháng, khi tăng tần số của dòng điện xoay chiều thì hệ số công suất của mạch

      A. không thay đổi                B. tăng                             C. giảm                              D. bằng 0

Lời giải
\(RLC: \ \ Z_L>Z_C\Leftrightarrow L2 \pi f> \frac{1}{C2\pi f}\)
Tăng f ⇒Z_L tăng và Z_C giảm 
\(\Rightarrow (Z_L-Z_C)\) tăng 
\(\Rightarrow cos\varphi =\frac{R}{\sqrt{R^2+(Z_L-Z_C)^2}}\) giảm xuống 

Câu 4: Mạch RLC nối tiếp, cuộn dây thuần cảm, R là một biến trở, được mắc vào mạng điện xoay chiều có hiệu điện thế hiệu dụng và tần số không đổi. Khi \(R=R_0, \omega \neq \frac{1}{\sqrt{LC}}\); thì công suất trong mạch đạt cực đại. Tìm phát biểu sai?

      A. Mạch đang có hiện tượng cộng hưởng 
      B. U_R < U
      C. U_R = \(\frac{U}{\sqrt{2}}\)
      D. Mạch có thể có tính cảm kháng hoặc dung kháng.

Lời giải
\(\left\{\begin{matrix} R=R_0\\ \omega \neq \frac{1}{\sqrt{LC}}\\ P_{max} \end{matrix}\right.\Rightarrow\) Mạch không xảy ra cộng hưởng điện

Câu 5: Mạch RLC mắc nối tiếp được mắc vào mạng điện có giá trị hiệu điện thế hiệu dụng không đổi, nhưng tần số có thể thay đổi. Khi tăng tần số của dòng điện thì công suất của mạch giảm. Tìm phát biểu đúng nhất?

      A. Mạch tính cảm kháng                                              B. Mạch có tính dung kháng
      C. Mạch đang cộng hưởng                                           D. Hệ số công suất của mạch nhỏ nhất

Lời giải
Mạch RLC nối tiếp
Tăng f ⇒ P luôn giảm⇒ Công suất cực đại ⇔ P_max
Mạch xảy ra cộng hưởng điện

Câu 6: Mạch RLC mắc nối tiếp được mắc vào mạng điện xoay chiều có tần số không đổi. Nếu cuộn dây không có điện trở thì hệ số công suất của mạch cực đại khi nào?

      A. R = Z_L - Z_C                      B. R = Z_L                          C. R = Z_C                           D. Z_L = Z_C

Lời giải
\(RLC\Rightarrow (cos\varphi )_{max}=1\Rightarrow\) Xảy ra CHĐ
\(\Rightarrow Z_L=Z_C\)

Câu 7: Trong đoạn mạch xoay chiều RLC nối tiếp, tụ điện có điện dung thay đổi được. Giả sử có hai giá trị C₁ và C₂ của tụ điện có công suất tiêu thụ trong mạch như nhau và với giá trị của điện dung là C₀ thì công suất tiêu thụ trong mạch cực đại. Mối liên hệ giữa C₁, C₂, C₀.

            A. \(\frac{2}{{{C_1}}} + \frac{2}{{{C_2}}} = \frac{1}{{{C_0}}}\)                       B. \(\frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} = \frac{2}{{{C_0}}}\)
             C. 2C₁ + 2C₂  = C₀                            D. C₁ + C₂ = 2C₀

Lời giải
\(\left\{\begin{matrix} C_1, C_2\Rightarrow P_1=P_2\\ C_0\Rightarrow P_{max} \end{matrix}\right.\Rightarrow Z_{C_1}+Z_C_2=2Z_C_0\)
\(\Rightarrow \frac{1}{C_1}+\frac{1}{C_2}=\frac{2}{C_0}\)

Câu 8: Phát biểu nào sau đây là đúng với mạch điện xoay chiều có tần số góc ω và trong mạch chỉ có cuộn thuần cảm hệ số tự cảm L?

            A. Mạch không tiêu thụ công suất.
            B. Tổng trở của đoạn mạch bằng 1/(\(\omega\)L)
            C. Điện thế giữa hai đầu đoạn mạch sớm pha hay trễ pha so với cường độ dòng điện tùy thuộc vào thời điểm ta xét.
            D. Điện thế trễ pha so với cường độ dòng điện.

Lời giải
Mạch chỉ có \(L\Rightarrow \left\{\begin{matrix} P=0\\ cos\varphi =0 \end{matrix}\right.\)

Câu 9: Cho đoạn mạch xoay chiều C, L, R mắc nối tiếp với nhau theo thứ tự trên. Độ lệch pha giữa hiệu điện thế u giữa hai đầu đoạn mạch và cường độ dòng điện là φ. Công suất tiêu thụ trên đoạn LC nối tiếp là:

            A. 0.                             B. UIcosφ                   C. (Z_L + Z_C)I²               D. |Z_L - Z_C|I²

Lời giải
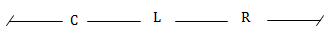Đoạn mạch LC có \(cos\varphi =0\)
\(\Rightarrow P=0\)

Câu 10: Chọn ý sai. Đặt vào hai đầu mạch điện RLC nối tiếp một hiệu điện thế u = U₀cosωt (không đổi) thì điện áp hiệu dụng trên các phần tử R, L và C đều bằng nhau. Khi thay điện trở R bằng điện trở R’ = 2R thì

            A. công suất tiêu thụ của mạch giảm.               B. hệ số công suất mạch giảm.
            C. tổng trở của mạch tăng.                               D. độ lệch pha giữa u và i không đổi.

Lời giải
\(RLC: u=U_0cos\omega t\)
\(u_R=U_L=U_C \Rightarrow\) Xảy ra cộng hưởng điện
\(R'=2R\)
\(U'_L=U'_C\Rightarrow\) vẫn xảy ra CHĐ

Câu 11: Đoạn mạch điện xoay chiều chỉ có tụ điện hoặc chỉ có cuộn cảm thuần đều

            A. có dòng điện qua mạch chậm pha hơn điện áp hai đầu mạch.
            B. có dòng điện qua mạch cùng pha \(\frac{\pi}{2}\) điện áp hai đầu mạch.
            C. không tiêu thụ công suất.
            D. có dòng điện qua mạch nhanh pha  so với điện áp hai đầu mạch.

Lời giải
Mạch chỉ có C hoặc chỉ có L đều không tiêu thụ công suất

Câu 12: Khi nói về hệ số công suất cosφ của đoạn mạch điện xoay chiều, phát biểu nào sau đây sai?

            A. Với đoạn mạch chỉ có tụ điện hoặc chỉ có cuộn cảm thuần thì cosφ = 0.
            B. Với đoạn mạch có R, L, C mắc nối tiếp đang xảy ra cộng hưởng thì cosφ = 0.
            C. Với đoạn mạch chỉ có điện trở thuần thì cosφ = 1.
            D. Với đoạn mạch gồm tụ điện và điện trở thuần mắc nối tiếp thì 0 < cosφ < 1.

Lời giải
\(0\leq cos\varphi \leq 1;cos\varphi =\frac{R}{\sqrt{R^2+Z^2_{LC}}}\)
Mạch RLC xảy ra CHĐ \(\Rightarrow cos\varphi =1\)

Câu 13: Mạch xoay chiều gồm cuộn dây thuần cảm L mắc nối tiếp với tụ điện có điện dung C và biến trở R. Đặt vào hai đầu mạch điện áp \(u = U_0cos2\pi ft\) thì thấy \(LC=\frac{1}{4\pi^2 f^2}\). Khi thay đổi giá trị của R thì

            A. hệ số công suất của mạch thay đổi.
            B. công suất tiêu thụ của mạch không đổi.
            C. điện áp hai đầu biến trở không đổi.
            D. độ lệch pha giữa điện áp hai đầu mạch với dòng điện thay đổi.

Lời giải
\(\left\{\begin{matrix} RLC:u=U_0cos 2 \pi f t \ \ \ \ \ \ \ \ \ \ \\ LC=\frac{1}{4\pi^2f^2}\Rightarrow Xay \ ra \ CHD \end{matrix}\right.\)
Thay đổi R ⇒ Vẫn xảy ra CHĐ 
⇒ U₂ = U (không đổi)
Câu 14: Cho đoạn mạch điện xoay chiều RLC mắc nối tiếp. Biết cảm kháng lớn hơn dung kháng; Điện áp giữa hai đầu mạch có giá trị hiệu dụng và tần số luôn không đổi. Nếu cho điện dung C tăng thì công suất tiêu thụ của đoạn mạch sẽ

            A. tăng đến một giá trị cực đại rồi lại giãm.      B. không thay đổi.
            C. luôn tăng.                                                    D. luôn giảm.

Lời giải
\(RLC: \ Z_L>Z_C\)
\(\Rightarrow Z_L-Z_C>0\)
+ Tăng C ⇒ Z_C giảm ⇒ (Z_L - Z_C) tăng 
\(\Rightarrow P=R.\frac{U^2}{R^2+(Z_L-Z_C)^2}\) giảm
Câu 15: Mạch xoay chiều RLC nối tiếp, với R thay đổi được. Khi cho R tăng dần từ vài Ôm lên vài trăm Ôm, hệ số công suất đoạn mạch

            A. giảm.                       B. tăng.                        C. không đổi.               D. giảm rồi tăng.

Lời giải
\(cos\varphi =\frac{R}{\sqrt{R^2+Z_{LC}^2}}=\frac{1}{\sqrt{1+\frac{Z^2_{LC}}{R^2}}}\)
⇒ Tăng R ⇒ \((\frac{Z_{LC}}{R})^2\) giảm ⇒\((cos\varphi )\) tăng 

Câu 16: Cho đoạn mạch xoay chiều gồm một điện trở R, một tụ điện có điện dung C biến đổi và một cuộn dây chỉ có hệ số tự cảm L mắc nối tiếp với nhau. Điện áp tức thời giữa hai đầu đoạn mạch là: u_AB = U₀cos \(\omega\) t . Công suất mạch cực đại Pmax ứng với giá trị C₀. Như vậy

            A. chỉ có một giá trị C > 0 có công suất P < P_max.
            B. hai giá trị C > C₀ có cùng công suất P < P_max.
            C. khi P_max thì \(\omega =\sqrt{LC_0}\) .
            D. khi P_max thì U_0R = U₀.

Lời giải
\(RLC: C\)
\(C=C_0\Rightarrow P_{max}\Rightarrow\) Cộng hưởng điện
\(\Rightarrow U_R=U\Rightarrow U_{OR}=U_0\)

Câu 17: Đoạn mạch AB gồm một tụ điện C mắc nối tiếp với một biến trở. Điện áp giữa hai đầu đoạn mạch u_AB = U\(\sqrt{2}\) cos \(\omega\)t. Điều chỉnh con chạy để biến trở có giá trị R = R₀ thì công suất tỏa nhiệt trên biến trở max. Lúc này

            A. P_max =\(\frac{U^2}{R_0}\)               B. R₀ = 2Z_C                  C. cos\(\varphi\)= 0,707          D. U_R = U

Lời giải
RC:
\(R=R_0\Rightarrow P_{max}\Rightarrow \left\{\begin{matrix} R_0=Z_C\\ P_{max}=\frac{U^2}{2R_0}\\ cos\varphi =\frac{1}{\sqrt{2}}=0,707 \end{matrix}\right.\)

Câu 18: Mạch xoay chiều gồm điện trở R và tụ điện điện dung C. Điện áp giữa hai đầu đoạn mạch u_AB = U \(\sqrt{2}\)cos \(\omega\)t . Khi tần số mạch tăng 4 lần thì

            A. dung kháng mạch tăng 4 lần.                       B. điện áp sẽ trễ pha so với dòng điện i.
            C. hệ số công suất của mạch tăng lên.             D. công suất mạch tiêu thụ tăng 4 lần.

Lời giải
RC: f tăng 4 lần ⇒ Z_C giảm 
\(cos\varphi =\frac{R}{Z}=\frac{R}{\sqrt{R^2+Z^2_C}}\)
\(\Rightarrow Z_C\) giảm \(\Rightarrow (cos\varphi )\) tăng

Câu 19: Cho mạch điện xoay chiều  không phân nhánh gồm: điện trở thuần R, cuộn dây thuần cảm có độ tự cảm L, tụ điện có điện dung C không đổi, mắc nối tiếp. Đặt vào hai đầu mạch một hiệu điện thế xoay chiều có hiệu điện thế hiệu dụng (U \(\neq\) 0) không đổi và có biểu thức u = U₀sin(\(\omega\) t +\(\varphi\)), thì có hiện tượng cộng hưởng. Tăng dần tần số thì

            A. hệ số công suất của đoạn mạch giảm.         B. cường độ hiệu dụng của dòng điện tăng,
            C. điện áp hiệu dụng trên tụ không đổi              D. điện áp hiệu dụng trên tụ điện tăng.

Lời giải
RLC: Xảy ra cộng hưởng điện \(\Rightarrow f_0=\frac{1}{2\pi \sqrt{LC}}\)
Tăng f ⇒ không còn CHĐ
⇒ Hệ số công suất \((cos\varphi )\) giảm

Câu 20: Cho đoạn mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Biết cảm kháng lớn hơn dung kháng ; Điện áp giữa hai đầu đoạn mạch có giá trị hiệu dụng và tần số luôn không đổi. Nếu cho điện dung C tăng thì công suất tiêu thụ của đoạn mạch sẽ

            A. tăng đến một giá trị cực đại rồi lại giảm.      B. không thay đổi.
            C. luôn tăng.                                                  D. luôn giảm.

Lời giải
\(Z_L>Z_C\Rightarrow Z_L-Z_C>0\)
Tăng C ⇒ Z_C giảm ⇒ (Z_L - Z_C) tăng 
\(P=R.\frac{U^2}{R^2+(Z_L-Z_C)^2}\)
\(\Rightarrow (Z_L-Z_C)\) tăng ⇒ P giảm