Câu 1: Lúc  t = 0 s đầu O của dây cao su căng thẳng nằm ngang bắt đầu dao động đi lên từ vị trí cân bằng theo chiều dương với biên  độ  U₀ =  1,5cm, chu kì T = 2s. Hai  điểm gần nhau nhất trên dây dao  động cùng pha  cách nhau 6 cm. Tại t = 1 s M cách O 1,5 cm có tốc độ dao động bằng bao nhiêu?

            A. v_M = 1,5\(\pi\) cm/s                                           B. v_M = -1,5\(\pi\) cm/s
            C. v_M = 0 cm/s                                                 D. Không thể xác định được

Lời giải
\(u_O=U_0cos(\omega t+\varphi _0)\)
\(U_0=1,5cm;\omega =\frac{2\pi}{T}=\pi\frac{rad}{s}\)
\(t=0\left\{\begin{matrix} u_0=0\\ v>0 \end{matrix}\right.\Rightarrow \varphi =-\frac{\pi}{2}\)
\(\lambda =6cm\)
\(\Rightarrow u_M=1,5.cos(\pi t - \frac{\pi}{2}-\frac{2\pi.1,5}{6})(cm)\)
\(\Rightarrow u_M=1,5.cos(\pi t - \pi)(cm)\)
\(\left\{\begin{matrix} t=1s\\ \left | v_M \right | =\left | v'_M \right |=\left | -1,5 \pi .sin(\pi .1 - \pi) \right | =0 \end{matrix}\right.\)
⇒ Chọn C
 

Câu 2: Một người ngồi ở bờ biển trông thấy có 10 ngọn sóng qua mặt trong 36 giây, khoảng cách giữa hai ngọn sóng liên tiếp là 10 m. Tính tần số sóng biển và vận tốc truyền sóng biển ?

            A. 0,25 Hz; 2,5 m/s     B. 4 Hz; 25 m/s           C. 25 Hz; 2,5 m/s        D. 4 Hz; 25 cm/s

Lời giải
\(9T=36s\Rightarrow T=4s\Rightarrow f=\frac{1}{T}=0,25Hz\)
\(\lambda =10m\Rightarrow v=\lambda .f=2,5\frac{m}{s}\)
⇒ Chọn A

Câu 3: Một người quan sát một chiếc phao trên mặt biển thấy phao nhấp nhô lên xuống tại chỗ 16 lần trong 30 giây và khoảng cách giữa 5 đỉnh sóng liên tiếp nhau bằng 24m. Tốc độ truyền sóng trên mặt biển là

            A. v = 4,5 m/s             B. v = 12 m/s.              C. v = 3 m/s                 D. v = 2,25 m/s

Lời giải
\(\left.\begin{matrix} 15T=30s\Rightarrow T=2s\\ 4\lambda =24m\Rightarrow \lambda =6m \end{matrix}\right\}\Rightarrow v= \frac{\lambda }{T}=3\frac{m}{s}\)
⇒ Chọn C

Câu 4: Một chiếc phao nhô lên cao 10 lần trong 36 s, khoảng cách hai đỉnh sóng lân cận là 10 m. Vận tốc truyền sóng là

            A. 25/9(m/s)                B. 25/18(m/s)              C. 5(m/s)                     D. 2,5(m/s)

Lời giải
\(\left.\begin{matrix} 9T=36s\Rightarrow T=4s\\ \lambda =10m \end{matrix}\right\}\Rightarrow v=\frac{\lambda }{T}=2,5\frac{m}{s}\)
⇒ Chọn D
 

Câu 5: Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số 120 Hz, tạo ra sóng ổn định trên mặt chất lỏng. Xét 5 gợn lồi liên tiếp trên một phương truyền sóng, ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm 0,5 m. Tốc độ truyền sóng là

            A. 30 m/s                     B. 15 m/s                     C. 12 m/s                     D. 25 m/s

Lời giải
\(\left.\begin{matrix} f=120Hz\\ 4\lambda =0,5m\Rightarrow \lambda =0,125m \end{matrix}\right\}\Rightarrow v=\lambda .f=15\frac{m}{s}\)
⇒ Chọn B
 

Câu 6: Nguồn phát sóng S trên mặt nước tạo dao động với tần số f = 100 Hz gây ra các sóng tròn lan rộng trên mặt nước. Biết khoảng cách giữa 7 gợn lồi liên tiếp là 3 cm. Vận tốc truyền sóng trên mặt nước bằng

            A. 25 cm/s.                  B. 50 cm/s.                  C. 100 cm/s                 D. 150 cm/s.  

Lời giải
\(\left.\begin{matrix} f=100Hz\\ 6\lambda =3m\Rightarrow \lambda =0,5m \end{matrix}\right\}\Rightarrow v=\lambda .f=50\frac{m}{s}\)
⇒ Chọn B
 

Câu 7: Tại O có một nguồn phát sóng với với tần số f = 20 Hz, tốc độ truyền sóng là 1,6 m/s. Ba điểm thẳng hàng A, B, C nằm trên cùng phương truyền sóng và cùng phía so với O. Biết OA = 9 cm; OB = 24,5 cm; OC = 42,5 cm. Số điểm dao động cùng pha với A trên đoạn BC là

            A. 1.                            B. 2.                            C. 3.                            D. 4.

Lời giải
\(f=120Hz; V=1,6\frac{m}{2}=160\frac{cm}{s}\Rightarrow \lambda =\frac{v}{f}=8cm\)

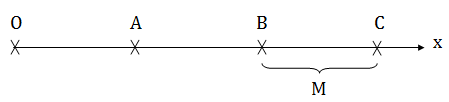
OA = 9cm; OB = 24,5cm; OC = 42,5cm
Điểm M cùng pha với \(A\Rightarrow AM=k.\lambda\)
\(\Rightarrow AB\leq k\lambda \leq AC\Rightarrow BO-AO\leq k\lambda \leq CO-AO\)
\(\Rightarrow 15,5\leq K.8\leq 33,5\Rightarrow 1,...\leq k\leq 4,...\)
\(\Rightarrow k=2,3,4\Rightarrow\) có 3 điểm thỏa yêu cầu bài tập
⇒ Chọn C

Câu 8: Trên mặt nước đang có sóng, ta thấy khoảng cách giữa hai gợn sóng liên tiếp là 10cm và một chiếc lá nhỏ trên mặt nước nhô lên liên tiếp 3 lần trong thời gian 5s. Tốc độ truyền sóng trên mặt nước là:

            A. 6cm/s.                     B. 2cm/s.                     C. 4cm/s.                     D. 8cm/s.

Lời giải
\(\left.\begin{matrix} \lambda =10cm\\ 2T=5s\Rightarrow T=2,5s \end{matrix}\right\}\Rightarrow v=\frac{\lambda }{T}=4\frac{cm}{s}\)
⇒ Chọn C
 

Câu 9: Một sóng ngang có biểu thức truyền sóng trên phương x là: u = 3cos(314t - x) m. Trong đó t tính bằng s, x tính bằng m. Bước sóng \(\lambda\) là:

           A. 8,64 cm                    B. 8,64m                      C. 6,28 m                     D. 3,14 m

Lời giải
\(u=3cos(314t-x)(m)\)
\(\frac{2\pi x}{\lambda }=x\Rightarrow \lambda =2 \pi=6,28m\)
⇒ Chọn C

Câu 10: Một sóng truyền dọc theo trục Ox có phương trình u = 0,5cos(10x - 100\(\pi\)t) (m)trong đó t tính bằng giây, x tính bằng m. Vận tốc truyền của sóng này là

      A. 100 m/s.                          B. 62,8 m/s.                C. 31,4 m/s.                D. 15,7 m/s.

Lời giải

\(u=0,5.cos(10x-100 \pi t)(m)\)
\(v=\frac{100 \pi}{10}=10 \pi=31,4\left ( \frac{m}{s} \right )\)
⇒ Chọn C

Câu 11: Một nguồn O phát sóng cơ dao động theo phương trình u₀ = 2cos(20\(\pi\)t + \(\frac{\pi}{3}\)) cm (trong đó u tính bằng đơn vị cm, t tính bằng đơn vị s). Xét sóng truyền theo một đường thẳng từ O đến điểm M với tốc độ không đổi 1m/s. Trong khoảng từ O đến M có bao nhiêu điểm dao động ngược pha với dao động tại nguồn O? Biết M cách O một khoảng 45cm.

      A. 4.                                    B. 3.                           C. 2.                            D. 5.

Lời giải
\(u_0=2.cos(20\pi t +\frac{\pi}{3})(cm);\lambda =\frac{100}{10}=10cm\)
+ Ngược pha \(\Rightarrow d=(k+\frac{1}{2})\lambda \Rightarrow 0< d=(k+\frac{1}{2})\lambda < 45\)
\(\Rightarrow -\frac{1}{2}< k< \frac{45}{10}-\frac{1}{2}=4\)
\(\Rightarrow k=0,1,2,3\)
⇒ Chọn A

Câu 12: Một nguồn sóng cơ học dao động điều hòa theo phương trình u = U₀cos(10\(\pi\)t + \(\pi\)/2) cm. Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng mà tại đó dao động của hai  điểm lệch pha nhau \(\pi\)/3 là 5m. Tốc độ truyền sóng là

      A. 75 m/s                             B. 100 m/s                   C. 6 m/s                    D. 150 m/s

Lời giải
\(u=U_0.cos(10 \pi t + \frac{\pi}{2})(cm)\)
\(\frac{2\pi d}{\lambda }=\frac{\pi}{3}\Rightarrow \lambda =6.d=30m\)
\(v=\lambda .f=30.5=150\frac{m}{s}\)
⇒ Chọn D
 

Câu 13: Phương trình sóng trên phương OX cho bởi: u = 2cos(7,2\(\pi\)t + 0,02\(\pi\)x) cm. Trong đó, t tính bằng s. Li độ sóng tại một điểm có tọa độ x vào lúc nào đó là 1,5 cm thì li độ sóng cũng tại điểm đó sau đó 1,25s là:

      A. 1cm                                B. 1,5cm                          C. - 1,5cm                 D. - 1cm

Lời giải
\(u=2.cos(7,2 \pi t + 0,02 \pi x)(cm)\)
\(t_1: u_1=2.cos(7,2 \pi t_1 + 0,02 \pi x)=1,5 cm\)
\(t_2=t_1+1,25s\Rightarrow u_2=?\)
\(T=\frac{2\pi}{\omega }=\frac{2\pi}{ 7,2 \pi }=\frac{1}{3,6}=\frac{5}{18}\)
\(\Rightarrow \frac{\Delta t}{T}=\frac{1,25}{\frac{5}{18}}=\frac{90}{20}=4,5\Rightarrow \Delta t=4,5T\)
\(\Rightarrow u_2=-u_1=-1,5cm\)
⇒ Chọn C
 

Câu 14: Một sóng cơ học được truyền theo phương Ox với tốc độ 20cm/s. Cho rằng khi truyền sóng biên độ không đổi. Biết phương trình sóng tại O là: u_O = 4cos(\(\pi\)t/6) cm, li độ dao động tại M cách O 40cm lúc độ dời sóng tại O đạt cực đại là:

      A. 4cm                                B. 0                                C. -2cm                        D. 2cm

Lời giải
\(v=20\frac{cm}{s}\Rightarrow \lambda =v.T=240cm\)
\(u_0=4cos(\frac{\pi t}{6})(cm)\Rightarrow T=12s\)
\(OM=40cm\rightarrow \left\{\begin{matrix} u_0=4cm\\ u_M=? \end{matrix}\right.\)
\(\Rightarrow u_M=4cos(\frac{\pi}{6}t-\frac{2\pi .40}{240})\)
\(\Rightarrow u_M=4cos(\frac{\pi}{6}t-\frac{\pi}{3}) \ (cm)\)
\(u_0=4cm\Rightarrow \frac{\pi}{6}t=0\Rightarrow u_M=2(cm)\)
⇒ Chọn D
 

Câu 15: Hai điểm M; N cùng nằm trên phương truyền sóng cách nhau \(\lambda\)/3. Tại thời điểm t có u_M = 3cm và u_N = - 3cm. Sau thời gian nhỏ nhất \(\Delta\)t bằng bao nhiêu kể từ t₁ thì u_M = U₀ (với U₀ là biên độ sóng), biết sóng truyền từ N đến M

      A. \(\frac{11T}{12}\)                               B. \(\frac{T}{12}\)                              C. \(\frac{T}{6}\)                                 D. \(\frac{T}{3}\)

Lời giải
\(t_1:\left\{\begin{matrix} u_M=3cm\\ u_N=-3cm \end{matrix}\right.\)
\(\left\{\begin{matrix} u_M=U_0\\ \Delta t_{min}=T-\frac{T}{12} \end{matrix}\right.=\frac{11T}{12}\)
⇒ Chọn A
 

Câu 16: Nguồn sóng ở O dao động với tần số 10Hz, dao động truyền đi với vận tốc 0,4m/s trên phương Oy. Trên phương này có 2 điểm P và Q theo thứ tự đó PQ = 15cm. Cho biên độ a = 1cm và biên độ không thay đổi khi sóng truyền. Nếu tại thời điểm nào đó P có li độ 1cm thì li độ tại Q là:

     A. 0                                     B. 2 cm                            C. 1cm                               D. - 1cm

Lời giải
\(f=10Hz;v=0,4\frac{m}{s}=40\frac{cm}{s}\Rightarrow \lambda =4cm\)
\(\frac{PQ}{\lambda }=\frac{15}{4}\Rightarrow PQ=15\frac{\lambda }{4}\Rightarrow\) u_P vuông u_Q
\(\Rightarrow u^2_P+u^2_Q=a^2=1\)
\(u_P=1\Rightarrow u_Q=0\)
⇒ Chọn A

Câu 17: Một sóng hình sin truyền theo phương Ox từ nguồn O với tần số 20 Hz, có tốc độ truyền sóng nằm trong khoảng từ 0,7 m/s đến 1 m/s. Gọi A và B là hai điểm nằm trên Ox, ở cùng một phía so với O và cách nhau 10 cm. Hai phần tử môi trường tại A và B luôn dao động ngược pha với nhau. Tốc độ truyền sóng là

      A. 90 cm/s.                          B. 80 cm/s.                      C. 85 cm/s.                        D. 100 cm/s.

Lời giải
\(d=AB=(2k+1)\frac{\lambda }{2}=(2k+1)\frac{v}{2f}\)
\(v=\frac{2.d.f}{2k+1}=\frac{400}{2k+1}\frac{cm}{s}\)
Mà \(70< v=\frac{400}{2k+1}<100\Rightarrow \left\{\begin{matrix} k=2\\ v=80 \frac{cm}{s} \end{matrix}\right.\)
⇒ Chọn B
 

Câu 18: Một dây đàn hồi rất dài có đầu A dao động với tần số f theo phương vuông góc với sợi dây với tốc độ truyền sóng v = 20 m/s. Hỏi tần số f phải có giá trị nào để một điểm M trên dây và cách A một đoạn 1 m luôn luôn dao động cùng pha với A. Cho biết tần số 20 Hz \(\leq\) f \(\leq\) 50 Hz.

      A. 10 Hz hoặc 30 Hz          B. 20 Hz hoặc 40 Hz       C. 25 Hz hoặc 45 Hz        D. 30 Hz hoặc 50 Hz

Lời giải​
\(d=AM=k\lambda =k.\frac{v}{f}\Rightarrow v=\frac{df}{k}\)
\(\Rightarrow f=\frac{k.v}{d}=\frac{k.20}{1}=10k\)
Mà \(20\leq f=20k \leq 50\)
\(\Rightarrow \bigg \lbrack \begin{matrix} f=20Hz\\ f=40Hz \end{matrix}\)
⇒ Chọn B

Câu 19: Cho sóng lan truyền dọc theo một đường thẳng. Cho phương trình dao động ở nguồn O là u₀ = acos\(\omega\)t. Một điểm nằm trên phương truyền sóng cách xa nguồn bằng bước sóng, ở thời điểm bằng chu kỳ thì có độ dịch chuyển là 5(cm). Biên độ

      A. 5,8(cm)                           B. 7,7(cm)                       C. 10(cm)                          D. 8,5(cm)

Lời giải​​
\(u_0=a.cos(\omega t)\)
\(\Rightarrow u_M=a.cos(\omega t - \frac{2\pi}{\lambda }.\frac{\lambda }{3})=a.cos(\omega t -\frac{2\pi}{3})\)
\(t=\frac{T}{2}\Rightarrow \left | u_M \right |=\left | a.cos(\omega .\frac{T}{2}-\frac{2\pi}{3}) \right |=5cm\)
\(\Rightarrow a\left | cos\frac{\pi}{3} \right |=5\Rightarrow a=10cm\)
⇒ Chọn C
 

Câu 20: Một sóng cơ học lan truyền trong một môi trường từ nguồn O với biên độ truyền đi không đổi. Ở thời điểm t=0, điểm O đi qua vị trí cân bằng theo chiều dương. Một điểm M cách nguồn một khoảng bằng 1/6 bước sóng có li độ 2cm ở thời điểm bằng 1/4 chu kỳ. Biên độ sóng là:

      A. 2 cm.                              B. 4 cm.                           C. 5 cm.                             D. 6 cm.

Lời giải
\(u_0=a.cos(\omega t+\varphi _0)\)
\(t=0\left\{\begin{matrix} u_0=0\\ v>0 \end{matrix}\right.\Rightarrow \varphi _0=-\frac{\pi}{2}\)
\(\Rightarrow u_0=a.cos(\omega t-\frac{\pi}{2})\)
\(\Rightarrow u_M=a.cos(\omega t-\frac{\pi}{2} -\frac{2\pi}{\lambda } .\frac{\lambda }{6})\)
\(\Rightarrow u_M=a.cos(\omega t -\frac{2\pi}{6 })\)
\(\left\{\begin{matrix} t=\frac{T}{4}\\ u_M=a.cos(\omega .\frac{T}{4}-\frac{5\pi}{6})=2(cm) \end{matrix}\right.\)
\(\Rightarrow a.cos(\frac{\pi}{2}-\frac{5\pi}{6})=2cm\Rightarrow a=4cm\)
⇒ Chọn B