Câu hỏi trắc nghiệm (40 câu):
-
Câu 1: Mã câu hỏi: 418172
Bất phương trình \(2{{x}^{2}}.3\text{x < 1}\) có bao nhiêu nghiệm nguyên?
- A. Có 1 nghiệm nguyên
- B. Có vô số nghiệm nguyên
- C. Không có nghiệm nguyên
- D. Có 2 nghiệm nguyên
-
Câu 2: Mã câu hỏi: 418173
Cho hàm số \(y={{x}^{3}}-6{{\text{x}}^{2}}+18\). Khẳng định nào sau đây đúng?
- A. Đồ thị hàm số không có tâm đối xứng
- B. Hàm số đồng biến trên \(\mathbb{R}\)
- C. Đồ thị hàm số không cắt parabol \(y=1-6{{\text{x}}^{2}}\)
- D. Giá trị cực đại của hàm số là \(18\)
-
Câu 3: Mã câu hỏi: 418176
Cho a,b là các số thực dương và \(a\ne 1\). Khẳng định nào sau đây đúng?
- A. \({{\log }_{\sqrt{a}}}\left( {{a}^{2}}+ab \right)=2+2{{\log }_{a}}\left( a+b \right)\)
- B. \({{\log }_{\sqrt{a}}}\left( {{a}^{2}}+ab \right)=4{{\log }_{a}}\left( a+b \right)\)
- C. \({{\log }_{\sqrt{a}}}\left( {{a}^{2}}+ab \right)=1+4{{\log }_{a}}b\)
- D. \({{\log }_{\sqrt{a}}}\left( {{a}^{2}}+ab \right)=4+2{{\log }_{a}}b\)
-
Câu 4: Mã câu hỏi: 418178
Tìm tất cả các giá trị của tham số a để đường thẳng \(\Delta :y=-x+a\)không có điểm chung với đồ thị (C ) của hàm số \(y=\frac{x-3}{x-2}\).
- A. Với mọi \(a\in \mathbb{R}\backslash \left\{ 0 \right\}\)
- B. \(a<1\)
- C. Với mọi \(a\in \mathbb{R}\)
- D. Không có giá trị của a
-
Câu 5: Mã câu hỏi: 418182
Hàm số nào dưới đây có tập xác định là \(\mathbb{R}\)?
- A. \(y=\frac{1}{x}\).
- B. \(y=\frac{x-1}{x+1}\).
- C. \(y=\frac{2\text{x}-1}{{{x}^{2}}+1}\).
- D. \(y=x\sqrt{x}-3\text{x}+1\).
-
Câu 6: Mã câu hỏi: 418185
Tìm giá trị nhỏ nhất m của hàm số \(y=\frac{1}{4}{{x}^{4}}+2017{{\text{x}}^{2}}+1\) .
- A. \(m=0\).
- B. \(m=2017\).
- C. \(m=\frac{1}{4}\).
- D. \(m=1\).
-
Câu 7: Mã câu hỏi: 418187
Hàm số nào sau đây có đồ thị như hình vẽ?
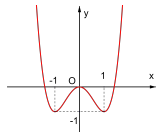
- A. \(y=-{{x}^{4}}+2{{\text{x}}^{2}}-3\)
- B. \(y={{x}^{4}}-2{{\text{x}}^{2}}-3\)
- C. \(y={{x}^{4}}-2{{\text{x}}^{2}}\)
- D. \(y={{x}^{3}}-3\text{x}-1\)
-
Câu 8: Mã câu hỏi: 418191
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, \(AB=a,AC=a\sqrt{3}\), cạnh bên SA vuông góc với đáy, \(SA=2\text{a}\). Khẳng định nào sau đây sai?
- A. Diện tích tam giác SBC bằng \(\dfrac{{{a}^{2}}\sqrt{10}}{2}\)
- B. Thể tích khối chóp S.ABC bằng \(\dfrac{{{a}^{3}}\sqrt{3}}{3}\)
- C. Chiều cao của hình chóp kẻ từ đỉnh A bằng \(\dfrac{2a\sqrt{5}}{5}\)
- D. Hình chóp có tất cả các mặt bên đều là tam giác vuông
-
Câu 9: Mã câu hỏi: 418193
Cho khối lập phương có diện tích toàn phần bằng 150. Tính thể tích V của khối lập phương đó .
- A. \(V=\frac{125}{3}\).
- B. \(V=27\).
- C. \(V=125\).
- D. \(V=64\).
-
Câu 10: Mã câu hỏi: 418196
Một hình nón có chiều cao bằng a và thiết diện qua trục là tam giác vuông. Tính diện tích xung quanh của hình nón.
- A. \(\frac{\pi {{a}^{2}}\sqrt{2}}{2}\).
- B. \(\pi {{a}^{2}}\sqrt{2}\).
- C. \(2\pi {{a}^{2}}\sqrt{2}\).
- D. \(2\pi {{a}^{2}}\).
-
Câu 11: Mã câu hỏi: 418198
Điểm cực tiểu của hàm số \(y={{x}^{3}}-3{{x}^{2}}+1\) là
- A. \(x=2\).
- B. \(y=1\).
- C. \(y=-3\).
- D. \(x=0\).
-
Câu 12: Mã câu hỏi: 418200
Gọi\({{x}_{1}},{{x}_{2}}\) là hai nghiệm của phương trình \({{\log }_{\sqrt{2}}}\left( {{4}^{x}}-{{3.2}^{x+1}}+2 \right)=2\text{x}+4\). Tính \({{x}_{1}}+{{x}_{2}}\)
- A. \({{x}_{1}}+{{x}_{2}}=1\).
- B. \({{x}_{1}}+{{x}_{2}}=7\).
- C. \({{x}_{1}}+{{x}_{2}}=10\).
- D. \({{x}_{1}}+{{x}_{2}}=0\).
-
Câu 13: Mã câu hỏi: 418202
Hàm số \(y={{x}^{2}}\ln {x} \) có bao nhiêu cực trị?
- A. 3 điểm.
- B. 1 điểm.
- C. Không có điểm nào.
- D. \(x=0\).
-
Câu 14: Mã câu hỏi: 418206
Tính thể tích khối lăng trụ tam giác đều có tất cả các cạnh bằng a.
- A. \(\frac{{{a}^{3}}\sqrt{3}}{12}\).
- B. \(\frac{{{a}^{3}}}{2}\).
- C. \(\frac{{{a}^{3}}\sqrt{3}}{4}\).
- D. \(\frac{{{a}^{3}}\sqrt{3}}{2}\).
-
Câu 15: Mã câu hỏi: 418210
Cho hình chóp S.ABC có ba cạnh SA,SB,SC đôi một vuông góc với nhau, \(SA=1,SB=2,SC=3\). Tính khoảng cách từ S đến mặt phẳng (ABC)
- A. \(h=\sqrt{14}\).
- B. \(h=\frac{\sqrt{14}}{2}\).
- C. \(h=\frac{6}{7}\).
- D. \(h=\frac{3\sqrt{14}}{7}\).
-
Câu 16: Mã câu hỏi: 418212
Viết phương trình tiếp tuyến của đồ thị hàm số \(y={{x}^{3}}-3\text{x}-1\) biết tiếp tuyến song song với đường thẳng \(\Delta :y=9\text{x}-17\)
- A. \(y=9\text{x + 15,}y=9\text{x}-17\)
- B. \(y=9\text{x+15}\)
- C. \(y=9\text{x + }17\)
- D. \(y=9x-\text{15,}y=9\text{x}-17\)
-
Câu 17: Mã câu hỏi: 418214
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD
- A. \(\frac{a}{\sqrt{3}}\).
- B. \(\frac{a}{3}\).
- C. \(\frac{a\sqrt{21}}{4}\).
- D. \(\frac{a\sqrt{21}}{6}\).
-
Câu 18: Mã câu hỏi: 418217
Gọi \(M\left( {{x}_{0}};{{y}_{0}} \right)\) là điểm chung của hai đồ thị hàm số \(y={{x}^{2}}-1\) và \(y=\frac{x+1}{3}\) thỏa mãn \({{x}_{0}}>0\). Tính giá trị của biểu thức \(A=\frac{1}{3}{{x}_{0}}+2{{y}_{0}}\)
- A. \(\frac{5}{3}\).
- B. \(4\).
- C. \(\frac{5}{9}\).
- D. \(2\).
-
Câu 19: Mã câu hỏi: 418221
Hàm số nào sau đây có đồ thị như hình vẽ?
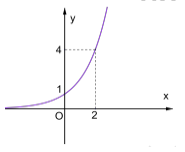
- A. \(y={{2}^{-x}}\).
- B. \(y={{\left( \frac{1}{2} \right)}^{-x}}\).
- C. \(y={{e}^{x}}\).
- D. \(y={{e}^{-x}}\).
-
Câu 20: Mã câu hỏi: 418222
Một người gửi tiền vào ngân hàng theo thể thức lãi kép với lãi suất 12% một năm, kì hạn là một tháng. Hỏi sau bao lâu , số tiền trong tài khoản của người đó gấp ba lần số tiền ban đầu
- A. 12 năm 5 tháng.
- B. 9 năm 3 tháng.
- C. 11 năm.
- D. 10 năm 2 tháng.
-
Câu 21: Mã câu hỏi: 418224
Tính đạo hàm của hàm số \(y={{2}^{{{x}^{2}}+1}}\)
- A. \(y'=\left( {{x}^{2}}+1 \right){{2}^{{{x}^{2}}}}\)
- B. \(y'={{2}^{{{x}^{2}}+1}}\)
- C. \(y'=x{{.2}^{{{x}^{2}}+2}}.\ln 2\)
- D. \(y'=\left( {{x}^{2}}+1 \right){{2}^{{{x}^{2}}+1}}\ln 2\)
-
Câu 22: Mã câu hỏi: 418227
Cho hình chóp tứ giác đều có cạnh đáy bằng a và thể tích bằng \(\frac{{{a}^{3}}}{3}\).Tính độ dài cạnh bên của hình chóp.
- A. \(a\).
- B. \(\frac{a\sqrt{3}}{2}\).
- C. \(\frac{a\sqrt{6}}{2}\).
- D. \(\frac{a\sqrt{3}}{3}\).
-
Câu 23: Mã câu hỏi: 418228
Một khối trụ có chu vi đường tròn đáy bằng \(12\pi a\), chiều cao bằng\(\frac{a}{2}\) Tính thể tích của khối trụ
- A. \(6\pi {{a}^{3}}\).
- B. \(12\pi {{a}^{3}}\).
- C. \(18\pi {{a}^{3}}\).
- D. \(24\pi {{a}^{3}}\).
-
Câu 24: Mã câu hỏi: 418230
Tìm giá trị nhỏ nhất của hàm số \(y={{e}^{{{x}^{2}}-2\text{x}}}\)trên đoạn \(\left[ 0;2 \right]\).
- A. \(e\).
- B. \(\frac{1}{{{e}^{2}}}\).
- C. \(1\).
- D. \(\frac{1}{e}\).
-
Câu 25: Mã câu hỏi: 418233
Cho hàm số\(y=\frac{2\text{x}+3}{x-1}\). Khẳng định nào sau đây là đúng?
- A. Hàm số có một điểm cực trị
- B. Hàm số không có giá trị nhỏ nhất
- C. Đường thẳng \(y=2\) là tiệm cận đứng của đồ thị hàm số
- D. Hàm số nghịch biến trên \(\mathbb{R}\)
-
Câu 26: Mã câu hỏi: 418235
Cho khối lăng trụ tam giác đều ABC.A’B’C’. Một khối trụ T nội tiếp khối lăng trụ đã cho. Gọi là thể tích khối trụ, \({{V}_{2}}\)là thể tích khối lăng trụ. Tính tỉ số \(\frac{{{V}_{1}}}{{{V}_{2}}}\)
- A. \(\frac{2\pi \sqrt{3}}{27}\).
- B. \(\frac{4\pi \sqrt{3}}{9}\).
- C. \(\frac{\pi \sqrt{3}}{9}\).
- D. \(\frac{\pi \sqrt{3}}{27}\).
-
Câu 27: Mã câu hỏi: 418238
Tìm tất cả các giá trị thực của tham số a để bất phương trình \(a\sqrt{{{x}^{2}}+6}<x+a\) nghiệm đúng với mọi giá trị thực của x
- A. \(a<-1\)
- B. \(a<1\)
- C. \(a=\frac{\sqrt{30}}{5}\)
- D. \(a<\frac{\sqrt{30}}{5}\)
-
Câu 28: Mã câu hỏi: 418240
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông, thể tích bằng V. Một khối nón có đỉnh là tâm của hình vuông ABCD, có đáy là hình tròn ngoại tiếp tứ giác A’B’C’D’. Tính thế tích khối nón
- A. \(\frac{\pi }{4}V\).
- B. \(\frac{\pi }{2}V\).
- C. \(\frac{\pi }{12}V\).
- D. \(\frac{\pi }{6}V\).
-
Câu 29: Mã câu hỏi: 418241
Tìm tập nghiệm S của phương trình \({{\log }_{2}}\left( x-1 \right)+{{\log }_{2}}\left( x+1 \right)=3\)
- A. \(S=\left\{ 3;-3 \right\}\).
- B. \(S=\left\{ \sqrt{7};-\sqrt{7} \right\}\).
- C. \(S=\left\{ 3 \right\}\).
- D. \(S=\left\{ 2 \right\}\).
-
Câu 30: Mã câu hỏi: 418243
Cho hàm số\(y=\frac{2x-1}{x+2}\)có đồ thị (C ). Tiếp tuyến của đồ thị (C ) tại điểm \(M\left( -1;-3 \right)\) tạo với hai đường tiệm cận của đồ thị (C ) một tam giác \(\Delta \). Khẳng định nào sau đây đúng?
- A. Tam giác \(\Delta \) có diện tích bằng 10
- B. Tam giác \(\Delta \) có chu vi bằng \(10+2\sqrt{26}\)
- C. Tam giác \(\Delta \) là tam giác vuông có một góc bằng \({{60}^{0}}\)
- D. Tam giác \(\Delta \) vuông cân
-
Câu 31: Mã câu hỏi: 418244
Có bao nhiêu giá trị nguyên của tham số m để phương trình\({{4}^{x}}-m{{.2}^{x}}+2m-5=0\)có hai nghiệm trái dấu?
- A. Có 2 giá trị nguyên
- B. Có 1 giá trị nguyên
- C. Không có giá trị nguyên nào
- D. Có vô số giá trị nguyên
-
Câu 32: Mã câu hỏi: 418245
Gọi n là số điểm trên đồ thị (C) của hàm số \(y=-2+\dfrac{1}{x-1}\) có hoành độ và tung độ là các số tự nhiên. Tìm n.
- A. \(n=2\).
- B. \(n=0\).
- C. \(n=4\).
- D. \(n=1\).
-
Câu 33: Mã câu hỏi: 418247
Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Tính thể tích khối tứ diện ACB’D’
- A. \(\frac{V}{3}\)
- B. \(\frac{V}{4}\)
- C. \(\frac{V}{6}\)
- D. \(\frac{V}{5}\)
-
Câu 34: Mã câu hỏi: 418248
Cho \({{\log }_{8}}3=a\) và \({{\log }_{3}}5=b\) . Tính \({{\log }_{10}}3\) theo a và b
- A. \(\frac{3\text{a}}{1+3\text{a}b}\).
- B. \(ab\).
- C. \(3\text{a}+b\).
- D. \(\frac{1}{a+3b}\).
-
Câu 35: Mã câu hỏi: 418249
Tính giá trị của biểu thức \(A=\frac{1}{{{\log }_{2}}2016!}+\frac{1}{{{\log }_{3}}2016!}+...+\frac{1}{{{\log }_{2016}}2016!}\)
- A. \(2016\).
- B. \(0\).
- C. \(2015\).
- D. \(1\).
-
Câu 36: Mã câu hỏi: 418251
Tìm số nghiệm của phương trình \({{2}^{\frac{1}{x}}}+{{2}^{\sqrt{x}}}=3\)
- A. Có 1 nghiệm
- B. Có 2 nghiệm
- C. Có vô số nghiệm
- D. Không có nghiệm
-
Câu 37: Mã câu hỏi: 418253
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=-{{x}^{3}}+3\text{x}+1\) tại giao điểm của đồ thị với trục tung
- A. \(y=1\).
- B. \(y=3\text{x}-1\).
- C. \(y=3\text{x + }1\).
- D. \(y=-3\text{x + }1\).
-
Câu 38: Mã câu hỏi: 418255
Tập xác định của hàm số\(y={{x}^{\pi }}\) là
- A. \(\mathbb{R}\).
- B. \(\left[ 0;+\infty \right)\).
- C. \(\left( 0;+\infty \right)\).
- D. \(\mathbb{R}\backslash \left\{ 0 \right\}\).
-
Câu 39: Mã câu hỏi: 418256
Trong không gian cho hai đường thẳng a,b cắt nhau và góc giữa chúng bằng \({{60}^{0}}\). Tính góc ở đỉnh tạo bởi mặt nón tạo thành khi quay đường thẳng a quanh đường thẳng b.
- A. \({{120}^{0}}\).
- B. \({{60}^{0}}\).
- C. \({{45}^{0}}\).
- D. \({{30}^{0}}\).
-
Câu 40: Mã câu hỏi: 418258
Một khối trụ \({{T}_{1}}\) có thể tích bằng 40.Tăng bán kính của \({{T}_{1}}\) lên gấp 3 lần ta được khối trụ \({{T}_{2}}\). Tính thể tích của khối trụ \({{T}_{2}}\)
- A. \(300\).
- B. \(240\).
- C. \(360\).
- D. \(120\).






