-
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SD = \frac{{a\sqrt {17} }}{2}\), hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn AB. Tính chiều cao h của khối chóp H.SBD theo a.
- A. \(h = \frac{{\sqrt 3 a}}{2}\)
- B. \(h = \frac{{a\sqrt 3 }}{7}\)
- C. \(h = \frac{{a\sqrt {21} }}{2}\)
- D. \(h = \frac{{3a}}{5}\)
Lời giải tham khảo:
Đáp án đúng: A
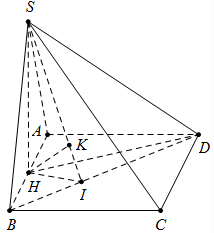
Từ H kẻ HI vuông góc với BD \(\left( {I \in BD} \right)\) và \(HK \bot SI\)
Suy ra \(HK \bot \left( {SBD} \right).\)
Ta có:
\(SH = \sqrt {S{D^2} - H{D^2}} = a\sqrt 3\) và
\(HI = \frac{{AC}}{4} = \frac{{a\sqrt 2 }}{4}\)
Suy ra \(HK = \frac{{SH.IH}}{{\sqrt {S{H^2} + I{H^2}} }} \)
\(= \frac{{\frac{{{a^2}\sqrt 6 }}{4}}}{{\frac{{5a\sqrt 2 }}{4}}} = \frac{{a\sqrt 3 }}{5}\)
Do đó chiều cao của khối chóp H.SBD là:
\(h = \frac{{a\sqrt 3 }}{5}.\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Trên cạnh SC lấy điểm E sao cho SE=2EC. Tính thể tích V của khối tứ diện SEBD. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1
- Cho khối lăng trụ ABC.A’B’C’ có thể tích V. Tính thể tích \(V_1\) của khối tứ diện A’B’C'C
- Cho hình chóp S.ABC có đáy là tam giác vuông cân có cạnh huyền là 4a và thể tích bằng \( a^3 \). Tính chiều cao h của khối chóp S.ABC
- Một kim tự tháp ở Ai Cập được xây dựng vào khoảng 2500 trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 150 m, cạnh đáy dài 220 m
- Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SD = \dfrac{{a\sqrt {17} }}{2}\), hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn AB. Tính chiều cao h của khối chóp H.SBD theo a.
- Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết hình chóp S.ABC có thể tích bằng \(a^3\). Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).
- Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Biết AC’ tạo với mặt phẳng (A'B'C) một góc 60^0 và AC' = 4a.
- Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh bằng a, góc \(\widehat{A}\) bằng \(60^0\) và cạnh bên AA’ = 2a. Tính thể tích V của khối hộp ABCD.A’B’C’D’.
- Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M là trung điểm của cạnh SD. Biết rằng khối chóp S.ABCD có thể tích bằng \(a^3\) và tam giác MAC là tam giác đều cạnh a, hãy tính khoảng cách d từ điểm S đến mặt phẳng (MAC).
- Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và SA=a. Điểm M thuộc cạnh SA sao cho \(\frac{{SM}}{{SA}} = k\). Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.







