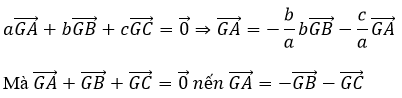-
Nếu ∆ABC đều thì a = b = c, điều kiện A đúng, B, C, D sai.
Ngược lại nếu
Do sự biểu thị duy nhất vectơ GA→ qua GB→ và GC→ nên \( - \frac{b}{a} = - \frac{c}{a} = - 1\)
=> a = b = c => ∆ABC đều. Chọn A.
Câu hỏi:Trong không gian với hệ tọa độ Oxyz, cho điểm \(M\left( {1;2;3} \right),\) gọi A,B và C lần lượt là hình chiếu vuông góc của M lên các trục Ox, Oy và Oz. Viết phương trình mặt phẳng \(\left( \alpha \right)\) qua ba điểm A,B và C.
Ta có: \(A\left( {1;0;0} \right),B\left( {0;2;0} \right),C\left( {0;0;3} \right) \Rightarrow \left( \alpha \right):\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1\,\)hay \(\,\left( \alpha \right):6x + 3y + 2z - 6 = 0.\)
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC VỀ PHƯƠNG TRÌNH MẶT PHẲNG
- Trong không gian với hệ tọa độ Oxyz, tìm một véctơ pháp tuyến n của mặt phẳng alpha
- Cho điểm H và mặt phẳng alpha cắt các trục tọa độ Ox, Oy và Oz tại các điểm A, B và C sao cho H là trực tâm của tam giác ABC
- Véc tơ nào dưới đây là một véc tơ chỉ phương của đường thẳng d
- Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d và mặt phẳng (P) biết đường thẳng d nằm trong mặt phẳng (P)
- Trong không gian Oxyz, mặt phẳng nào sau đây đi qua gốc tọa độ
- Trong các điểm sao đây, điểm nào thuộc mặt phẳng (Oyz)
- Viết phương trình mặt phẳng đi qua A, B và song song với trục Ox
- Hỏi có bao nhiêu mặt phẳng song song với đường thẳng d đồng thời cách đều A, B và d
- Viết phương trình mặt phẳng đi qua điểm M(2;-1;3) và song song với mặt phẳng 3x + 2y + z + 4 = 0.
- Viết phương trình mặt phẳng cách đều hai đường thẳng d và d'