Cho tam giác ABC nội tiếp đường tròn (O;R), đường cao AH. Biết rằng AB=12cm, AC=20cm, AH=10m. Độ dài bán kính của đường tròn là:

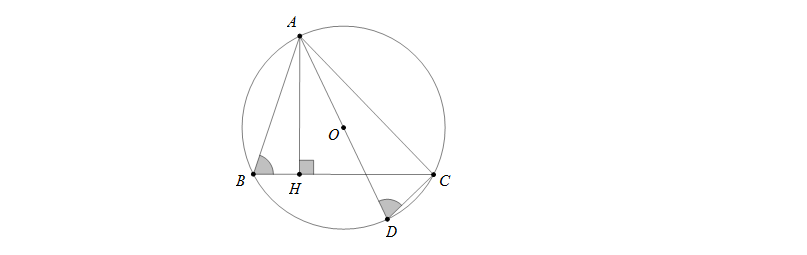
Vẽ đường kính AD của đường tròn thì AD=2R.

Khi đó góc ACD là góc nội tiếp chắn nửa đường tròn nên \(\widehat{ACD}=90^0\)

Xét hai tam giác vuông AHB và ACD có \(\widehat{ABH}=\widehat{ADC}\) (góc nội tiếp cùng chắn cung AC)

nên \(\bigtriangleup AHB \sim \bigtriangleup ACD\Rightarrow \frac{AB}{AD}=\frac{AH}{AC}\Rightarrow AB.AC=AH.2R\)

Theo đề bài ra suy ra \(R=\frac{AB.AC}{2.AH}=\frac{12.20}{2.10}=12 cm\)