-
Câu hỏi:
Cho tam giác ABC nhọn. Đường tròn đường kính BC cắt AB tại N, AC tại M. Gọi H là giao điểm của CN và BM. Khi đó A,N,H,M cùng nằm trên đường tròn nào?
- A. \((I;IM)\), I là trung điểm MN
- B. \((I;IH)\), I là trung điểm MN
- C. \((F;FA)\), F là giao điểm đường tròn với AH
- D. \((E;EA)\), E là trung điểm AH
Lời giải tham khảo:
Đáp án đúng: D
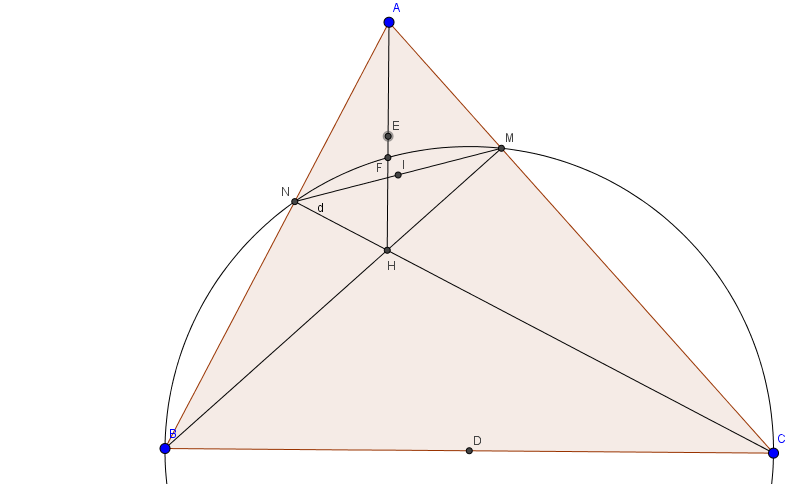
Trước tiên: hai tam giác BNC và BMC là hai tam giác lần lượt vuông tại N và M. Đường tròn đường kính BC đi qua M,N
Xét hai tam giác ANH và AMH cũng lần lượt vuông tại N,M. Với E là trung điểm AH, Ah là cnahj huyền của cả hai tam giác
nên đường tròn tâm E bán kính EA sẽ đi qua M, N, H.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Cho hai đường thẳng xy và xy cuông góc với nhau cắt nhau tại O.Một đoạn thẳng AB=8 chuyển động sao cho A luôn nằm trên xy và B luôn nằm x'y'
- Cho hình thang ABCD (ABparallel CD), widehat{C}=widehat{D}=60^{circ}, CD=2AD=8. Khi đó A, B, C, D luôn thuộc đường tròn nào?
- Cho tam giác ABC có BH, CE là các đường cao. Gọi M là giao điểm BH và CE. I là trung điểm BC. Khi đó B,C,E,H cùng thuộc đường tròn nào?
- Cho đường tròn tâm A đường kính BC. Gọi D là trung điểm AB. Dây EF vuông góc với AB tại D. Tứ giác EBFA là hình gì?
- Cho tam giác ABC nhọn. Đường tròn đường kính BC cắt AB tại N, AC tại M. Gọi H là giao điểm của CN và BM. Khi đó A,N,H,M cùng nằm trên đường tròn nào?







