Cho hình chóp S.ABCD có đáy là hình vuông cạnh a SD=a căn 17/2 hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn AB

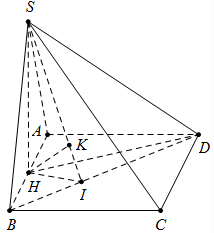
Từ H kẻ HI vuông góc với BD \(\left( {I \in BD} \right)\) và \(HK \bot SI\)  suy ra \(HK \bot \left( {SBD} \right).\)

Ta có \(SH = \sqrt {S{D^2} - H{D^2}} = a\sqrt 3\) và \(HI = \frac{{AC}}{4} = \frac{{a\sqrt 2 }}{4}\)

Suy ra  \(HK = \frac{{SH.IH}}{{\sqrt {S{H^2} + I{H^2}} }} = \frac{{\frac{{{a^2}\sqrt 6 }}{4}}}{{\frac{{5a\sqrt 2 }}{4}}} = \frac{{a\sqrt 3 }}{5}\)

Do đó chiều cao của khối chóp H.SBD là \(h = \frac{{a\sqrt 3 }}{5}.\)