-
Câu hỏi:
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
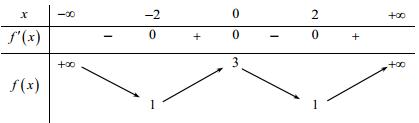
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
- A. \(\left( { - 2;{\mkern 1mu} {\mkern 1mu} 0} \right)\)
- B. \(\left( {2; + \infty } \right)\)
- C. \(\left( {0;{\mkern 1mu} {\mkern 1mu} 2} \right)\)
- D. \(\left( {0; + \infty } \right)\)
Lời giải tham khảo:
Đáp án đúng: C
Phương pháp giải:
Dựa vào BBT để nhận xét tính đơn điệu của hàm số.
+) Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( {a;\;b} \right) \Leftrightarrow f'\left( x \right) \ge 0\;\;\forall x \in \left( {a;\;b} \right).\)
+) Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {a;\;b} \right) \Leftrightarrow f'\left( x \right) \le 0\;\;\forall x \in \left( {a;\;b} \right).\)
Lời giải chi tiết:
Dựa vào BBT ta thấy hàm số nghịch biến trên các khoảng \(\left( { - \infty ;{\mkern 1mu} {\mkern 1mu} - 2} \right)\) và \(\left( {0;{\mkern 1mu} {\mkern 1mu} 2} \right).\)
Chọn C.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Đồ thị trong hình vẽ là đồ thị của hàm số nào
- Số tiếp tuyến của đồ thị hàm số \(y = {x^4} - 2{x^2} - 3\) song song với trục hoành
- Cho hàm số \(f\left( x \right)\) có bảng biến thiên. Hàm số đã cho nghịch biến trên khoảng nào
- Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng
- Tính tổng số mặt, số cạnh và số đỉnh của một hình lập phương?
- Hình hộp đứng ABCDA’B’C’D’ có đáy ABCD là hình thoi cạnh a, \(\widehat {ABC} = {120^0}\); \(AA' = 4a\). Tính k/c giữa A’C & BB’
- Đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x - 1}}\) có các đường tiệm cận đứng, tiệm cận ngang là bao nhiêu
- Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f\left( x \right) = {\left( {x + 1} \right)^2}\left( {2 - x} \right)\left( {x + 3} \right). Chọn mệnh đề đúng
- Tìm số điểm thuộc đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x - 1}}\) thỏa mãn tiếp tuyến với đồ thị tại điểm đó
- Tìm số giao điểm của đồ thị hàm số \(y = {x^4} - 2{x^2} + 1\) và đường thẳng \(y = 1\)
- Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy
- Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{x + 1 - \sqrt {3x + 1} }}{{{x^2} - 3x + 2}}\) là?
- Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích các mặt ABCD, ABB'A', ADD'A' lần lượt bằng \(36c{m^2}\), \(225c{m^2}\), \(100c{m^2}\). Tính thể tích khối A.A'B'D'?
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình: Đồ thị hàm số \(y = \left| {f\left( x \right) - 2m} \righ
- 1 đường thẳng cắt đồ thị hàm số \(y = {x^4} - 2{x^2}\) tại 4 điểm phân biệt có hoành độ \(0,{\mkern 1mu} 1,{\mkern 1m
- Đồ thị sau là của hàm số \(y = {x^4} - 3{x^2} - 3.\) Tìm m để phương trình \({x^4} - 3{x^2} - 3 = m\) có đúng 3 nghiệm phân biệt?
- Khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), \(SA = a\), \(AB = a\), \(AC = 2a\), \(BC = a\sqrt 3\). Tính thể tích SABC
- Đồ thị hàm số \(y = \dfrac{x}{{\sqrt {{x^2} - 1} }}\) có bao nhiêu đường tiệm cận?
- Xét các khẳng định sau. Số khẳng định đúng trong các khẳng định trên là?
- Cho I là tâm đối xứng của ĐTHS (y = \dfrac{{2x - 3}}{{x + 2}}\). Tìm tọa độ điểm \(I\)?
- Cho hình lập phương ABCD.ABCD. Góc giữa hai đường thẳng BC & BD là?
- Gọi M, m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = 2{x^3} + 3{x^2} - 1\) trên đoạn\(\left[ { - 2; - \dfrac{1}{2}} \right]\). Tìm \(P = M - m\)?
- Tìm số mặt của khối đa diện đều loại \(\left\{ {5;3} \right\}\)
- Cho HS \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) & có đạo hàm \(f'\left( x \right) = {\rm{\;}} - \left( {x - 10} \right){\left( {x - 11} \right)^2}{\left( {x - 12} \right)^{2019}}\). Tìm khẳng định đúngg?
- Cho hình chóp S.ABCD có đáy hình thoi cạnh a, \(\angle BAD = {60^0}\), cạnh bên \(SA = a\) và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ B đến mp \(\left( {SCD} \right)\)?
- Cho HS \(y = \dfrac{{x + 3}}{{ - 1 - x}}\). Tìm mệnh đề đúng
- Tìm GTNN của hàm số \(y = \dfrac{{{x^2} - 5}}{{x + 3}}\) trên \(\left[ {0;2} \right]?\)
- Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mp đáy, \(AB = 2a,{\mkern 1mu} {\mkern 1mu} \widehat {BAC} = {60^0}\) và \(SA = a\sqrt 2 .\) Góc giữa đt SB và mp \(\left( {SAC} \right)\) bằng?
- Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ. Mệnh đề nào sau đây sai?
- Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\left( {a;b} \right)\). Phát biểu nào sau đây là sai?
- Gọi \(A\left( {{x_1};{y_1}} \right)\), \(B\left( {{x_2};{y_2}} \right)\) là 2 điểm cực trị của đồ thị hàm số \(y = {x^3} - 3x -
- Đồ thị trong hình là của HS nào?
- Cho hàm số \(y = f(x)\) có đạo hàm \(f'\left( x \right) = 2018{\left( {x - 1} \right)^{2017}}{\left( {x - 2} \right)^{2018}}{\left( {x - 3} \right)^{2019}}\). Tìm số điểm cực trị của \(f(x)\)?
- Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 3;4} \right]\) & có đồ thị như hình vẽ
- Khẳng định nào dưới đây về hàm số \(y = {\rm{\;}} - {x^4} - 3{x^2} + 2\) là đúng?
- Cho hình chóp S.ABC có \(A',{\mkern 1mu} {\mkern 1mu} B'\) lần lượt là trung điểm của \(SA,{\mkern 1mu} {\mkern 1mu} SB\). Biết thể tích khối chóp S.ABC bằng 24. Tính thể tích \(V\) của khối chóp S.A'B'C?
- Cho biết bảng biến thiên ở hình dưới là của một trong 4 hàm số được liệt kê dưới đây.
- Cho hình chóp đều S.ABC có độ dài cạnh đáy là 2a, mặt bên tạo với mặt đáy một góc \({60^0}\). Tính thế tích của khối chóp S.ABC?
- Tìm m để đường thẳng \(y = 2x + m\) cắt đồ thị hàm số \(y = \dfrac{{x + 3}}{{x + 1}}\) tại hai điểm \(M,\;N\) sao cho đ�
- Cho khối chóp tam giác có V bằng 6. Gọi \(M,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} P\) là trung điểm các cạnh \(BC,{\mkern 1mu} {\mkern 1mu} CA,{\mkern 1mu} {\mkern 1mu} AB\). Tính V của S.MNP là?







